 | ||
 | ||
 | ||
 | ||
Руководитель: Андрей Заболотский
Участники:
Расул Баламамедов
Данила Брутер
Виталий Аллахвердянц
Для перехода из одной системы отсчета в другую существуют преобразования Галилея, основанные на том, что время во всех системах отсчета течет одинаково, а единственное преобразование – корректива на движение одной системы отсчета относительно другой. Назовем x и t – координату и время в системе, которую мы считаем неподвижной, а x’ и t’ –в движущейся относительно нее со скоростью v. Тогда, для перехода в «штрихованную» систему отсчета потребуются следующие преобразования:
t’ = t
x’ = x–vt
Это связано с тем, что за время t точка с координатой х в системе отсчета переместилась со скоростью v относительно неподвижной системы отсчета на расстояние vt.
Однако, преобразования Галилея неверны по следующей причине: согласно первому закону Ньютона существуют инерциальные системы отсчета, т.е. такие системы отсчета, в которых тела, на которые не действуют никакие силы (или они уравновешивают друг друга), находятся в состоянии покоя или равномерного движения. Вместе с тем, известен постулат о том, что любое взаимодействие имеет максимальную скорость распространения, в данном случае – это максимальная скорость распространения света (скорость света в вакууме), в дальнейшем обозначаемая как с.
Но тогда выясняется, что эта скорость должна быть одинаковой во всех системах отсчета вне зависимости от их движения, иначе это фундаментальное ограничение теряет смысл, если с можно превышать в некоторых системах отсчета. Тогда, надо сделать вывод, что время в различных системах отсчета течет по-разному.
Рассчитаем, как движение приводит к замедлению времени.
Предположим, что у нас есть зеркальная банка с расстоянием между поверхностями l.
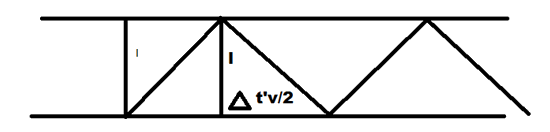
Вертикальная линия - траектория фотона, летающего между поверхностями в банке, неподвижной относительно нашей системы отсчета. Диагональная – в банке, движущейся со скоростью v.
Длина вертикального отрезка – l по условию, горизонтального отрезка – Δt’·v/2, где Δt’ – время, за которое свет пересек банку в два конца. По теореме Пифагора диагональная линия равна корню из суммы квадратов горизонтальной и вертикальной, но в тоже время, эта линия – расстояние, пройденное фотоном и равное сΔt’/2.
Составим уравнение:
(cΔt’/2)2 = l2 + (Δt’v/2)2
l2 + (Δt’v)2/4 = Δt’2c2/4
Δt’2 = -4 · l2/(v2 – c2)
Δt’ = 2l/sqrt(c2 – v2)
Δt’ = 2l/(c · sqrt(1 – v2/c2))
Но в тоже время, мы знаем, что Δt = 2l/c.
Δt’/Δt = 1 / sqrt(1 – v2/c2) = γ.
Таким образом, в системе отсчета, движущейся относительно нашей, свет вынужден проходить большее расстояние, а так как c неизменна в любой системе отсчета, то все процессы происходят с нашей точки зрения медленнее в γ раз.
Раз мы поняли, что положение о том, что время одинаково для всех систем отсчета неверно, то надо и заменить преобразования Галилея на учитывающие это преобразования Лоренца.
Преобразования Лоренца для линии имеют вид системы из двух уравнений:
t’ = a1t+b1x
x’ = a2t+ b2x
a и b – различные коэффициенты, зависящие от v и от c, но не зависящие от t и x. Таким образом, мы можем узнавать их значение в различных предельных случаях.
Например, подставим x = 0. Тогда ничего не меняется, так как мы всего лишь сели в начало нашей системы координат. Но t’ должно относится к t как γ, значит, a1 = γ.
Также, при x = 0 разделив верхнее уравнение на нижнее, получаем
x’ / t’ = a2/a1 = v
Подставим t = 0.
t’ = b1x
x’= b2x
x’/t’ = b1 / b2
Далее, подставим x’ = 0 и получим, что x / t = -a2/b2= -v
Значит, b2 = a1 = γ.
a2 = a1v = vγ.
Осталось лишь найти b1.
Переделываем уравнения, чтобы получать не x’ и t’ из x и t, а наоборот.
t = γt’ + b1(-v)x’
x = -γvt’ + γx’
Подставляем преобразования Лоренца в первое из этих уравнений:
t = γ(γt + b1(v)x) + b1(-v)·(γvt’ + xγ)
t = tγ2 + yxb1(v) + b1(-v)γvf + b1(-v)xγ
t = t(γ2 + b1(-v)vγ) +x(γb1(v) +γb1(-v))
Мы знаем, что в формуле t есть t, но нет x. В тоже время, мы знаем, что t = t, поэтому коэффициент при t равен 1, а коэффициент при x равен 0.
γ(b1(v) + b1(-v)) = 0, при γ ≠ 0.
b1(v) = -b1(-v)
Больше мы ничего не получили, поэтому, решаем первое уравнение.
γ2 + b1(-v) γv = 1
b1(-v) = (1 –γ2)/ γv
b1(-v) = (1 – 1/(1 – v2/c2))/ γv
Приводим к общему знаменателю:
b1(-v) = ((1 - v2/c2 – 1)/(1 – v2/c2))/ γv
b1(-v) = ((- v2/c2)/(1 – v2/c2))/ γv
Мы знаем, что 1 – v2/c2 = 1/γ2, и подставляем это в уравнение:
b1(-v) = (-v2/c2)/(1/γ2 · γv)
b1(-v) = -vγ/c2
Из первого уравнения системы мы знаем, что b1(v) = -b1(-v)
Подставляем это и получаем:
b1(v) = vγ/c2
Итого, получаем, что система уравнений, описывающая преобразования Лоренца имеет вид:
t’ = γt + γvx/c2
x’= γx + γvt
Несложно видеть, что при бесконечной скорости света или очень малой скорости v преобразования Лоренца сводятся к преобразованиям Галилея.
Формула сложения скоростей.
Существует система из машины и пули. Пуля движется со скоростью u в системе, где началом отсчета является машина, машина движется со скоростью v,следовательно, система движется со скоростью v. Найти скорость пули в системе координат, связанной с дорогой.
1) Разложение скоростей на оси x и y
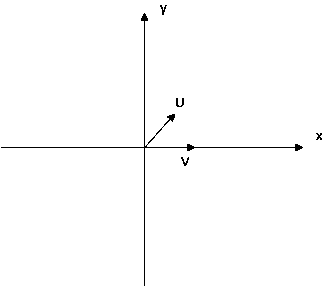
2) Переход в другую систему отсчета
t - временная координата по основной системе отсчета
t’ – временная координата относительно другой системы отсчета
x - координата пули по основной системе отсчета
y - координата пули по основной системе отсчета
x’ - координата пули относительно другой системы отсчета
y’ - координата пули относительно другой системы отсчета
ux - проекция скорости пули по оси x
uy - проекция скорости пули по оси y
v - скорость машины
γ=1/√(1-v2/с2) - релятивистский фактор
x’= uxt’, y’= uyt’ при y=y’
Применив преобразования Лоренца , получаем данные формулы
γ(t’+v/c2·x)=uxγ(t+v/c2·x)
y=uy γ(x+vt)
3) Нахождение x/t и y/t
y = uy·γt(1-v2)/c2/(1-ux·u)/v2c2)
y = uy·t √((1-v2)/c2)/(1-ux·v/с2)
y/t = uy/ γ(1-ux·v/c2)
x’= γ(x+vt) = ux(t+v/c2·x)
x+vt = uxγ(t+v/c2·x)
x-ux·v/c2·x = uxt-vt
x(1-ux·v/c2) = t(ux-v)
x/t = (ux-v)/(1- ux·v/c2)
[Напоминаем, что пройденный путь (в данной ситуации координата по каждой из 2 осей) поделенный на затраченное время = скорость.]
Ранее мы рассмотрели преобразования Лоренца для одномерной системы координат. Теперь сделаем это для двумерной системы отсчета.
Главная проблема, с которой нам придется столкнуться – это то, что если в одномерной системе отсчета любая скорость направлена вдоль оси координат, то в двух- и более- мерных системах отсчета это может быть не так. Чтобы с этим справимся, введем к системе отсчета (x,y) систему отсчета (x~, y~), отличающуюся от нее поворотом на угол θ.
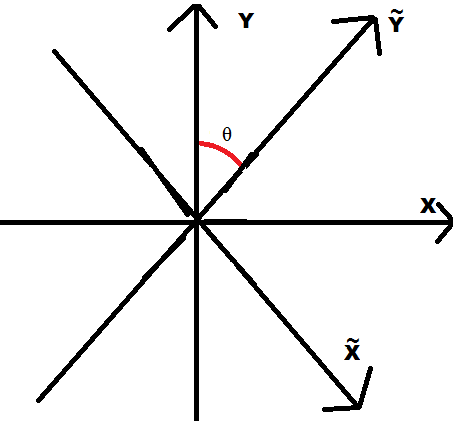
Наша задача – найти, как перейти из системы отсчета в сдвинутую на угол θ, так, чтобы ось x~ совпадала с вектором скорости, затем провести преобразования Лоренца и сдвинуть систему отсчета обратно на угол -θ.
Сначала опишем преобразования для перехода из системы отсчета (x, y) в систему отсчета (x~, y~). Т.к. системы неподвижны одна относительно другой, то t~ = t.
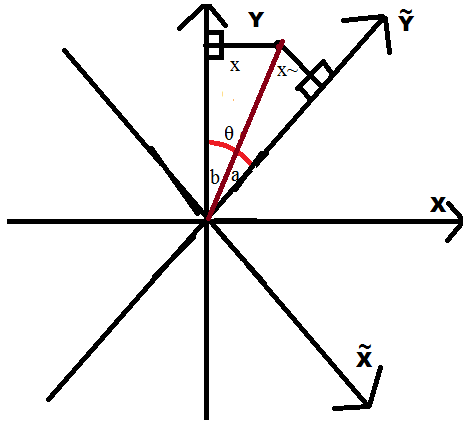
На этом рисунке видно, что x и x~ являются катетами в двух прямоугольных треугольниках с общей, а значит – равной гипотенузой.
x~ = x · sin(θ - b)/sin(b)
x~ = x · sin(θ - arcsin(x/sqrt(x2 + y2))/(x/(sqrt(x2 + y2)).
x~ = sin(θ - arcsin(x/sqrt(x2 + y2)) · sqrt(x2+y2)
x~ = sqrt(x2+y2)·(sinθ·y/ sqrt(x2+y2) – x/ sqrt(x2+y2)·cosθ)
x~ = -sinθ·y + cosθ·x
Аналогично, напишем такое же соотношение для y:
y~ = cosθ·y +sinθ·x
Ура! Мы научились переходить из системы отсчета в повернутую на угол θ (и обратно).
Запишем исходные уравнения преобразований Лоренца для движения по оси x (оно ничем не отличается от уже описанного движения в одномерной системе координат):
y’ = y
t’ = γt+γvx/c2
x’= γx + γvt
Поворачиваем систему отсчета на угол θ.
Получаем:
y~’ = cosθy +sinθx
x~’ = γx·cosθ – yγ·sinθ + vtγ
t’ = tγ + γv/c2(-sinθy + cosθx)
Смещаем систему отсчета обратно – на угол -θ.
sin(-θ) = -sinθ, а cos(-θ) = cosθ.
Получаем:
y’ = cosθ·(cosθy +sinθx) – sinθ·(γx·cosθ– yγ·sinθ+ vtγ)
t’ = tγ + γv/c2(-sinθy + cosθx)
x’ = (cosθy +sinθx)sinθ + (γx·cosθ – yγ·sinθ + vtγ)cosθ.
Обращаем внимание, что ничего плохого в том, что t зависит от x~, т.к. это выделенное направление – вдоль него направлен вектор скорости.
Это и есть преобразования Лоренца для двумерной системы координат.
Практика показывает, что преобразования Лоренца гораздо удобнее в векторном виде, нежели в том, в котором мы его получили.
Например, это позволяет записать преобразования Лоренца вне зависимости от количества измерений.
Запишем переход к векторам для y:
y’ = y·cosθ2+x·sinθ·cosθ – (γx·sinθ·cosθ–γy·sin2θ+vtγ·sinθ)
y’ = y·(cos2θ+γ·sin2θ)+x·sinθ·cosθ(1 – γ)–vtγ·sinθ
y’ = y·(cos2θ+ (1+γ-1)γ·sin2θ)+x·sinθ·cosθ(1 – γ)–vtγ·sinθ
y’ = y+y(γ-1)sin2θ+x·sinθ·cosθ(1 –γ) – vtγ·sinθ
y’ = y+(γ-1)(sin2θy-x·sinθ·cosθ) – vtγ·sinθ
y’ = y+(γ-1)(sinθ·y-x·cosθ)sinθ – vtγ·sinθ
Методом шаманства мы предполагаем, что в ответе будет содержатся скалярное произведение r·v.
r·v = ((x, y) · (v·cosθ, -v·sinθ))=xv·cosθ-yv·sinθ=v(x·cosθ – y·sinθ)
Подставляем это в уравнение и получаем, что:
y’ = y + (γ – 1)·sinθ·(r·v)/v – vtγ·sinθ
Аналогично, для x получаем:
x’ = x + (γ – 1)·cosθ(r·v)/v + vtγ·cosθ
Мы видим, что единственное отличие в замене x на y, и cosθ на -sinθ.
При этом, cosθ = vx/v, а -sinθ=vy/v
Объединяем уравнения и получаем
r’ = r+(γ-1)(r·v)v/v2 + vtγ
Суть в том, что vx и vy дают вместе v, и их модули сокращаются, но v в числителе остается, т.к. величина векторная, а вектор со скаляром нельзя сокращать.
Далее, с t все гораздо проще.
t’ = tγ+γv(-sinθ·y+cosθ·x)/c2
t’ = tγ + γ·(r·v)/c2
Таким образом, мы получили преобразования Лоренца в векторном виде.
Если бы второй закон Ньютона F = mA был бы верен в этом виде, то при достаточной силе тело бы разгонялось до сверхсветовых скоростей.
На самом деле выглядит второй закон Ньютона следующим образом: F = p•
А p при релятивистских скоростях равно не mv, а пространственной компоненте четырехмерного вектора импульса, и, следовательно, p = mγ(vx,vy,vz) = mvγ
Второй закон Ньютона мы уже получили, но хотим помимо этого сделать уравнение v(t) для решения чисто конкретных задач.
Для этого надо исходить из предположения, что сила со временем не меняется. Получаем, что v = p·sqrt(1 – v2/c2)/m
При этом, p(t) = Ft, и тогда уравнение сводится после упрощения к следующему виду:
v(t) = Ftc/sqrt(c2m2+(Ft)2)
Как это ни странно, существование электромагнетизма предсказывается именно СТО.
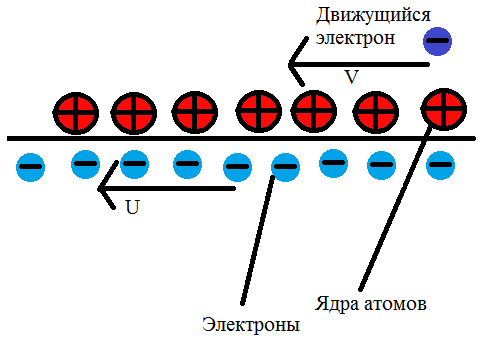
Пусть у нас есть провод под напряжением, по которому идет ток. Провод состоит из металла, который состоит из жесткой кристаллической решетки, в которой находятся неподвижные ядра атомов и общих электронов этой решетки, которые, т.к. по проводу идет ток, двигаются со скоростью u. Плотности электронов и ядер равны в системе отсчета провода, иначе бы провод был бы заряжен. Мимо летит электрон со скоростью v. Расстояние между электронами провода (т.к. они движутся) и расстояние между ядрами провода меняются в системе отсчета летящего мимо электрона неодинаково, а значит, с его точки зрения провод заряжен.
Рассчитаем этот эффект.
γ1 – отношение времени летящего электрона к времени электронов провода.
γ2 – отношение времени летящего электрона к времени ядер провода.
γ3 – отношение времени движущихся электронов к времени ядер атомов.
γ1 = 1/sqrt(1 – ((u – v)/(1 – vu/c2))2/c2))
Упрощаем и получаем:
γ1= (c2 – uv)/sqrt((c2 – v2)(c2 – u2))
γ2= 1/sqrt(1 – v2/c2)
γ3= 1/sqrt(1 – u2/c2)
При этом, известно, что длина участка с константным количеством электронов в системе отсчета летящего электрона равна
γ2/γ1 · γ3·l
Это верно, поскольку γ2/γ1 – отношение сокращения расстояния между электронами и расстояния между ядрами в системе отсчета летящего электрона, а γ3 –необходима, так как расстояние между ядрами в системе отсчета электронов провода также сокращается.
Получаем следующую формулу (без учета γ3 – его добавим позже)
lэлектронов/lядер = γ3 sqrt((c-v)(c+v)(c+u)(c-u)/((1-v/c)·(1+v/c)))/(c2-uv)
lэлектронов/lядер = γ3sqrt((c+u)(c-u))·с/(c2-uv)
lэлектронов/lядер = sqrt((c+u)(c-u))·с/(c2-uv)· 1/sqrt(1 – v2/c2).
lэлектронов/lядер = с2/(c2-uv).
Отношение плотностей обратно отношению длин, следовательно, отношение плотностей электронов и ядер провода в системе отсчета летящего электрона – следующее:
ρэлектронов/ρядер =(c2-uv)/с2.
Найдем плотность заряда провода в системе отсчета летящего электрона.
ρэлектронов-ρядер = ρядер((c2-uv)/с2 – 1) = ρядер· (- uv/c2)
Рассчитаем силу, с которой провод притягивает летящий электрон.
Притяжение точечного заряда к размазанному по линии равно
2qλ/r·ke
q – заряд точечного заряда (здесь – это заряд электрона), λ – плотность заряда на линии (только что найден нами), r – расстояние от летящего электрона до провода, ke– константа электростатического взаимодействия.
Подставляем в формулу и получаем:
F = qvkF·(-uke/cr) = qvBkF
Видимо, мы получили правильную формулу, т.к. ее можно привести к формуле действия магнитного поля на заряд qvBkF. А также, при v или u равном 0, F = 0, что также необходимо.
B = 2qρядерu/rc2·ke/kF
Также, если мы перемножим зарядовую плотность (мы в системе отсчета провода, поэтому ρядер = ρэлектронов), на скорость электронов провода, то получим силу тока I = qρядерu.
Тогда, получим, что B = 2I/rc2·ke/kF
Задача
Имеется световая волна, движущаяся только по оси x в вакууме.
Найти длину световой волны относительно движимой системы отсчета
λ – длина волны относительно начальной системы отчета
c – скорость света
T – период относительно начальной системы отчета
λ’ - длина волны относительно движимой системы отсчета
T’ - период относительно движимой системы отсчета
v – скорость, с которой движется движимая система отсчета
Eф - начальная энергия фотона
Eэ - начальная энергия электрона
pф - импульс фотона
pэ - импульс электрона
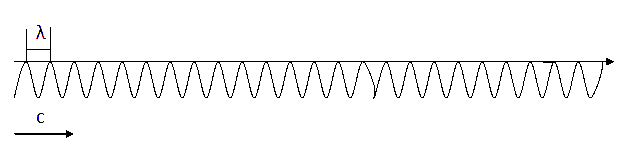
λ=cT
c=λ/T
λ’=(c-v)T’
λ’=( λ/T-v)T’
λ’/T’= λ/T-v
1/T’= (λ/T-v)/ λ’
T’= λ’/( λ/T-v)
λ’=(c-v)T’
λ’=(c-v)Tγ
λ’=(c-v)(λ/c)γ
λ’=(c-v)(λ/c)(1/sqrt(1-v2/c2))
В результате вычислений получаем численное выражение эффекта Доплера для нахождения длины волны относительно движущейся системы отсчета.
Далее используя формулы λ’=(c-v)(λ/c)(1/sqrt(1-v2/c2)) и Eф’=hν’ находим энергию фотона после удара с электроном.
λ’/c = 1/ν’
c/λ’ = ν’
c/(Eф’/h) = (c-v)(λ/c)(1/sqrt(1-v2/c2))
c(h/Eф’) = (c-v)(λ/c)(1/sqrt(1-v2/c2))
h/Eф’ = ((c-v) (λ/c)(1/sqrt(1-v2/c2)))/c
Далее преобразуем эту формулу для энергии и обобщим на случай изменения угла движения фотона:
Eф’ = Ec/((c - v cosα)γ) - Эффект Допплера
Задача
Нахождение энергии фотона после удара с электроном и отскока фотона в любом направлении
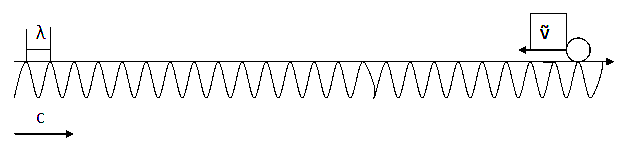
Используя систему центра масс:
Eф=pф(c-v)
Eэ=mэc2
Eэ+Eф=Eобщ
pф-pэ=0
0=(Eф’/c)-mэvγэ
Eф’= (сmэv)/sqrt(1-v2/c2)
Подзадача
Найти энергию фотона после удара с электроном при условии, что pф=pэ
В ходе преобразований получаем:
Eф’=(E·sqrt(1-v2/c2)/(c(c-v))
Eф’=Ec/((c-v)γ)
В результате вычислений получаем численное выражение рассеивания Комптона для нахождения энергии при условии, что pф = pэ
Далее вычисляем скорость движения системы:
pэ - pф = 0
(E/c)-mvγ=0
(Ecmγ)/(c-v)γ=v
E/γ = mvγ(c-v)
E/mγ=γ(vc-v2)
E/m=(vc-v2)/(1-v2/c2)
Ec + Ev = vm
v = Ec/(E-mc2)
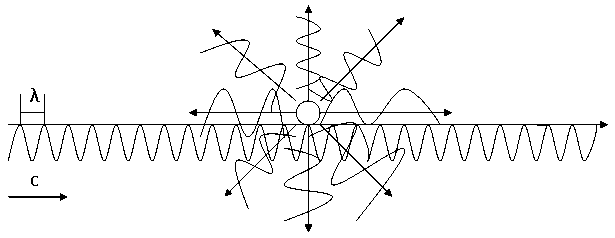
Eф’=(Emэc2)/(mc2-E(1+cosα)) - Рассеивание Комптона
Пущино, 2012 год.