 | ||
 | ||
 | ||
 | ||
Участники проекта:
Подоляко Федор,
Заболотский Андрей,
Петухов Матвей,
Фанасков Роман,
Кешелава Тимур.
Руководители проекта:
Березин Андрей Всеволодович
Лысов Иван Дмитриевич.
Наш проект был направлен на решение замысловатых физических задач, преимущественно с колебательным движением. В первый рабочий день мы составили список задач, из которого каждый мог выбрать задачу по вкусу. Многих заинтересовала задача про пружину и ее поведение в крайних точках, когда она растянута в проволоку или сжата до предела. Но по мнению преподов, эта была "неправильная" и сложная задача, и ее решено было не брать в качестве первой задачи. Выбор пал на две задачи: про веревку, подвешенную за два конца (Роман + Матвей), и про физический маятник (Тимур + Федор). Впоследствии, когда к нам присоединился Заболотский А.Д., появилось еще одно направление нашего проекта, получившее кодовое название "Шарик". ("Шарик падает на наклонную плоскость и прыгает. Вопрос, как он это делает?" - Подоляко Ф.) Далее тот же культовый персонаж МКШ, написав пару - тройку работающих программ, покинул партию "Маятник", оставив Тимура одного на попечение преподов, и стал заниматься авторской задачей про Шарик.
Черноголовка, 2005 год.
(Петухов Матвей, Фанасков Роман)
Нашей задачей было исследование верёвки, подвешенной за два конца, нахождение формы, которую она принимает. Мы исследовали случай, когда оба конца веревки находятся на одной высоте.
Далее мы используем следующие термины:
Ширина веревки - расстояние от одного конца веревки до другого.
Высота веревки - расстояние между прямой, на которой лежат концы веревки и нижней точкой этой веревки.
Идеальная верёвка - верёвка с нулевой жёсткостью.

Изначально была выдвинута гипотеза o том, что форма, принимаемая идеальной верёвкой, не зависит от свойств верёвки, как то: масса верёвки, её толщина и т.д. Для доказательства участники проекта подвешивали веревку к классной доске за два конца, обводили ее мелом по контуру и сравнивали результаты, полученные при подвешивании разных верёвок. Из нескольких веревок максимально подходящими для дальнейших опытов оказались обычная швейная нить и "Белая Гибкая" веревка. В дальнейшем для экспериментов мы использовали "Белую Гибкую" веревку. Эксперименты подтвердили вышеизложенную гипотезу.
Помимо этого начального вспомогательного исследования было поставлено три эксперимента по нахождению зависимости между различными параметрами веревки. В первом опыте была постоянна "ширина", во втором - "высота", а в третьем - длина веревки. О них читай далее.
Первой была проделана серия экспериментов, направленных на определение
зависимости между высотой и длиной веревки при постоянном расстоянии между
концами веревки. Для этого мы подвешивали веревку за два конца, между
которыми было постоянное расстояние в 100 см.. Этот эксперимент был весьма
трудоемким и занял продолжительное время, т.к. при больших значениях длины
веревки не хватало места на доске для измерений и пришлось воспользоваться
кабинетной стеной и стремянкой. Результат приведен ниже в виде графика.
См. рис. 1.
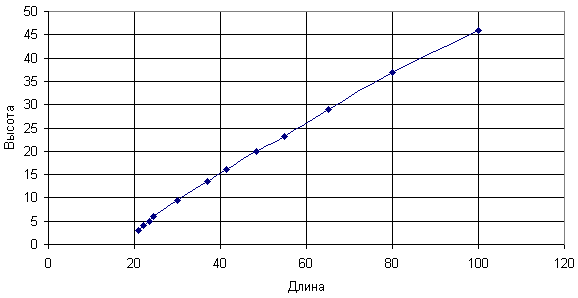
Рис. 1. Зависимость высоты от длины верёвки (расстояние между концами 100).
Следующим был эксперимент при постоянной "высоте" веревки, в котором мы
пытались определить, как меняется длина веревки при изменении расстояния
между ее концами. На нижеприведенном графике показана также прямая (х =
у), которая соответствует натянутой веревке, у которой расстояние между
концами равняется длине веревке. При достаточно больших значениях "ширины"
веревки график зависимости длины от ширины будет приближаться к этой
прямой. См. рис. 2.
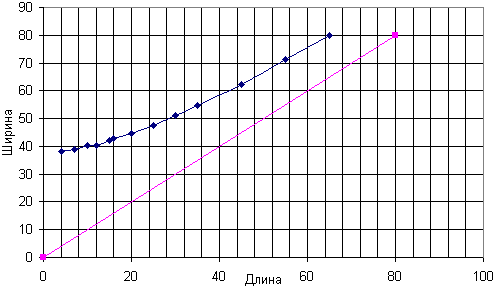
Рис. 2. Зависимость длины верёвки от расстояния между её концами (высота=90).
Последний эксперимент проводился аналогично двум другим, но в нем была
постоянна длина веревки. Значение координаты по оси Ох ("ширины") не может
превышать 175 см., т.е. длины веревки (веревка натянута, "высота" равна
0). Максимальное значение по оси Оу - 87.5 см., т.е. половина веревки
("ширина" равна 0, веревка висит вертикально).См. рис. 3.
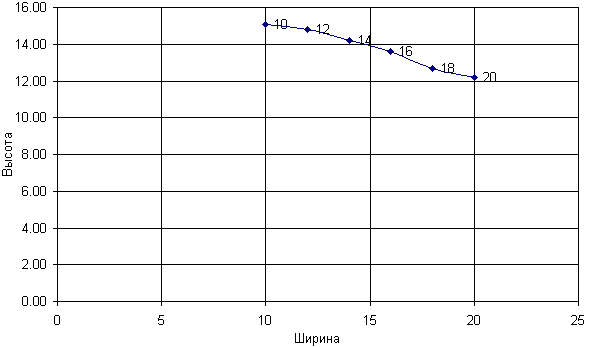
Рис. 3. Зависимость высоты от расстояния между концами верёвки (длина верёвки=175).
Помимо практических экспериментов, мы занимались теоретическим исследованием верёвки, подвешенной за 2 конца. Более того - изначально эксперименты были призваны лишь подтвердить или опровергнуть гипотезу о постоянстве формы верёвки, и только позднее они стали отдельной веткой партии "Верёвка".
Для начала было необходимо выбрать подходящую модель, по которой мы бы
исследовали верёвку. Такой моделью стали n одинаковых по длине отрезков
легкой нерастяжимой нити, которые связывают между собой n-1 массивных
шариков, сосредотачивающих в себе всю массу верёвки. При больших n
свойства такой модели приближаются к свойствам реальной верёвки.
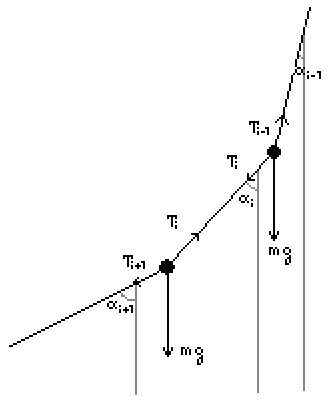
Рис. 4.
На чертеже показан участок такой модели верёвки. Как нетрудно видеть,
на каждый узел действует 3 силы - сила тяжести и 2 силы натяжения верёвки.
Каждый отрезок верёвки характеризуется углом с вертикалью. Для того чтобы
верёвка находилась в равновесии, в каждом i-ом узле должны выполняться
следующие уравнения:
|
Также использовались условия неразрывности нити, т.е.:
| Dl |
n S i=1 | sinai = D | (3) |
| Dl |
n S i=1 |
cosai = H = 0 | (4) |
После мы занялись написанием программы, которая бы по некоторым входным параметрам рисовала или хотя бы просчитывала форму верёвки. Фактически она должна была решать нелинейную систему из множества уравнений.
Для начала была написана программа, рассчитывающая углы и силы в верёвке, состоящей из двух нитей и одного узла. Делала она это методом простой итерации. Её написание не составило особого труда. Она представлена под названием Rope_simple. Однако при попытке превратить её в программу, делающую то же самое для n участков нити и n-1 узлов, не увенчались успехом. При n = 2 она ещё работала, но уже при n = 3 метод переставал сходиться.
При отладке были исправлены многие ошибки и добавлены новые, однако это не помогло. В результате, будучи не в силах признать свою беспомощность, мы обвинили в своих неудачах метод и стали искать новый. И он был найден. Суть его заключалась в том, что часть неизвестных в каждой итерации цикла решения системы мы выражали из уже найденных, а не из полученных в предыдущей итерации значений. Однако такая программа опять же не была рабочей.
После были внесены изменения в исходную систему уравнений. Было
замечено, что из уравнения (2) следует:
| (5) |
| (6) |
Следующая программа основывалась на решении системы уравнений (3), (4) и (6), однако также не была успешной.
Позднее мы выразили эти уравнения не через углы, характеризующие отрезки нити, а через координаты узлов, вернее через изменение координаты при переходе от узла к следующему, т. е.
|
|
|
Тогда, используя те же уравнения, мы применили другой метод - метод "стрельбы". Его суть в том, что мы случайно выбираем начальные a0 и C, строим верёвку с сохранением длины и вычисляем отклонение последней точки от заданного величиной D ("шириной" верёвки) положения и, изменяя a0 и C, подгоняем верёвку в нужное положение.
Этот метод также оказался дефективным и не сходился. Наутро предпоследнего дня последней рабочей недели участников проекта посетило вдохновение в лице руководителя проекта и предложило новую идею. К вечеру идея была уже обдумана, переработана и реализована. Именно она предлагается вниманию читателя под названием Rope_liambda_version.
Принцип её работы таков: мы задаём какой-то a0 и строим верёвку длины L, смотрим, куда попал конец верёвки, в зависимости от результатов подгоняем угол до тех пор, пока концы верёвки не окажутся на одном уровне. Считаем расстояние между концами верёвки и изменяем длину верёвки так, чтобы отношение длины верёвки к расстоянию между концами было таким же, как и в заданных изначально значениях. Потом повторяем до тех пор, пока координаты последней точки не совпадут с точностью e с ожидаемыми.
К сожалению, у нас не получилось сравнить экспериментальные результаты с полученными в программе. Однако первые люди, увидевшие результат, воскликнули "Это же цепная линия!", то есть та самая линия, которую мы ожидали. Поскольку воскликнувшие были преподавателями, мы считаем, что программа работает правильно.
(Заболотский Андрей, Подоляко Фёдор)
На наклонную плоскость падает шарик. Все параметры известны. Что будет дальше? (смоделировать ситуацию).
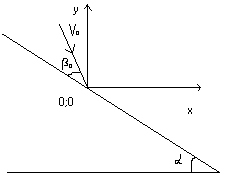
Рис. 5.
Пусть для начала нет ни трения, ни сопротивления воздуха; удар абсолютно упругий. Даны: угол наклона плоскости a, ускорение свободного падения g, скорость шарика V0 и угол его падения на плоскость b0. Возьмём систему координат с центром в точке падения шарика, оси координат направлены по x и по y соответственно вправо и вверх. Найти нужно скорость V1 и угол падения b1 шарика во время следующих ударов о плоскость, а также L1 - расстояние между точками ударов.
Угол падения на плоскость равен углу отражения от неё, поэтому когда шарик отскакивает от плоскости, его скорости по x и по y:
Vx0=V0cos(b0-a),
Vy0=V0sin(b0-a).
Время в полёте
t1=2(Vy0+Vx0tga)/g.
В момент второго удара скорости по x и по y:
Vx1=Vx0,
Vy1=Vy0-gt1,
а координаты таковы:
x=Vx0t1,
y=-x tga.
Тогда:
|
b1 = -a -
arctg(Vy1/Vx1)
|
Далее, учитывая, что в любой момент полёта x=Vx0t и y=Vy0-gt2/2, была написана программа, которая моделирует прыжки шарика по наклонной плоскости и записывает в файл данные о прыжках, а также рисует траекторию на экране.
Рассмотрим эффекты, связанные с вращением шарика.
Теперь исходные данные таковы: начальные скорости по x и по y - Vx0 и Vy0, начальная угловая скорость вращения - w0, коэффициент трения о плоскость cm, момент инерции J, радиус шарика R и его масса m, а также угол a и ускорение свободного падения g. Найти надо скорости по x и по y - Vx и Vy, и новую угловую скорость w, а также L1, для которого, впрочем, формула не изменилась.
Выведена система из 8 уравнений.
Кроме перечисленных переменных и параметров, в уравнениях фигурирует масса
Земли Mз, но её удалось исключить, положив равной бесконечности.
Дополнительные неизвестные Vxз, Vyз,
DPx, DPy и K
(соответственно скорости
Земли по x и по y, до удара равные 0, изменение импульса по x и по y и
изменение момента импульса) тоже были исключены. 5-ое уравнение представляет
собой закон сохранения энергии, первые 4 - закон сохранения импульса, 6-ое -
закон сохранения момента импульса, 7-ое выводится из закона сохранения
импульса следующим образом:
|
Здесь N - реакция опоры.
Доказательство восьмого уравнения:
DcK = FтрRDt = -DPxR
Итак, вот уравнения:
mVx0 = mVx+DPx
mVx0-mVx = MзVxз
mVy0 = mVy+DPy
mVy0-mVy = MзVyз
|
Jw0 = Jw-DK
DPx = -mDPy
DK = -DPxR = mDPyR
(уравнения выведены для случая =0)
Путём несложных выкладок были получены следующие решения:
|
|
|
Программа, моделирующая движение вертящегося шарика, написана.
Однако выяснилось, что для случая Vx+Rw = 0
(когда шарик катится) формула для расчёта силы трения не работает
(Px № mDPy). Из-за этого
угловая скорость расчитывается по следующей формуле:
w = -Vx/R. Отсюда:
|
Программы, созданные в ходе работы: tgraph.pas, bgraph2.pas.
(Кешелава Тимур, Подоляко Фёдор)
Нашей задачей было исследовать поведение физического маятника с помощью моделирующей программы и сравнить результаты с данными, полученными опытным путем.
1) Сначала мы занялись выводом формул для программы, составлением уравнений.
2) Потом мы написали программу, считавшую в координатах (x;y). В различных версиях программы (всего 5 версий), вводились различные параметры, такие как: угол отклонения от положения равновесия в радианах, шаг по времени, начальная скорость по Ох, задержка (программный параметр).
3) Далее программа была усовершенствована, в нее была добавлена
графика. Теперь она стала рисовать на экране движение нижней точки
маятника и ее траекторию. При большом шаге по времени программа начинала
рисовать непредсказуемые "узоры", где менялась длина нити, и ни о какой
реалистичности такого поведения маятника речи быть не могло. Это
происходило из-за того, что при большем шаге увеличивалась погрешность
вычислений. При достаточно малом шаге программа работает правильно. Полные
описания программ вы можете найти в дополнении 2.
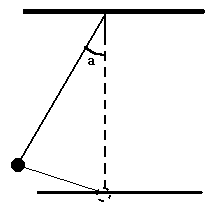
4) Теперь наступило время проверки теории на практике. Путем нескольких
хитрых махинаций участникам проекта удалось построить действующую модель
маятника в комнатных условиях.
Детали и компоненты установки:
а. Стремянка металлическая раскладная;
б. Небольшая доска с гвоздями;
в. Веревка, привязывающая доску к стремянке;
г. Веревка маятника, привязанная к доске с гвоздями;
д. Еще несколько веревок, удерживающих стремянку в неподвижном положении;
е. Пакет кефира в качестве груза маятника. Был выбран из-за заранее известной массы в 1кг. (была указана на пакете);
ж. Бутылка с водой 1.5л. как второй маятник. (первый был с аппетитом уничтожен участниками проекта);
з. Веревка, играющая роль горизонта;
и. Веревка для измерения отклонения маятника от точки равновесия.
Также при проведении эксперимента использовались секундомер и участники проекта. При проведении экспериментов никто не пострадал, кроме кефира.
5) Результаты экспериментов подтвердили правильность уравнений и компьютерной модели. См. дополнение.

Длина маятника = 1.5м. (const)
| Период, с. | Кол-во колебаний, шт. | Описание |
| 26.1 | 10 | a = 60°, смещение по хорде 1.5 м., масса маятника 1 кг., подвеска болтается. |
| 27.1 | 10 | |
| 27.2 | 10 | |
| 27.1 | 10 | |
| 26.0 | 10 | Смещение по хорде 1м., масса маятника 1 кг. |
| 26.2 | 10 | |
| 26.4 | 10 | |
| 26.1 | 10 | Смещение по хорде 0.5м., масса маятника 1 кг. |
| 26.0 | 10 | |
| 26.2 | 10 | |
| 28.5 | 10 | a = 90°, масса маятника 1 кг, подвеска немного качается. |
| 28.5 | 10 | |
| 28.5 | 10 | |
| 28.3 | 10 | |
| 25.4 | 10 | a = 60°, Смещение по хорде 1.5м., масса маятника 1.25 кг |
| 25.1 | 10 | Смещение по хорде 0.5 м., масса маятника 0.6 кг. |
| 25.0 | 10 | |
| 25.2 | 10 | |
| 25.6 | 10 | Смещение по хорде 1 м., масса маятника 0.6 кг. |
| 25.5 | 10 | |
| 25.6 | 10 | |
| 26.3 | 10 | Смещение по хорде 1.5 м., масса маятника 0.6 кг. |
| 26.0 | 10 | |
| 26.1 | 10 |
Это программа моделирует поведение одного маятника в декартовой системе координат. В этой программе надо ввести шаг по времени, скорость по Х и задержку. Это продукт имеет минус: надо вводить меленький шаг по времени, в противном случае, из-за ошибок округления маятник будет себя вести непредсказуемо.
Эта программа похожа на предыдущую, но только внешне (в ней надо вводить те же самые параметры). На самом деле эта версия намного лучше, т.к. она считает в полярной системе координат. Благодаря этому нововведению здесь не будет ошибок даже при достаточно большом шаге по времени.
Эта программа является вершиной (возможно, не очень красивой) эволюции компьютерных моделей одного маятника. Здесь не только расчет ведется в полярной системе координат, но и вместо линейной скорости вводится угол начального отклонения. Также в этой программе есть возможность посчитать период обращения, который с 3%-ой точностью совпадает с результатами опытов.
Эта программа разительно отличается от выше описанных версий. Главное отличие - это то, что маятников стало два. Первый прикреплен к неподвижному подвесу, а второй - к первому. Такое изменение делает задачу труднее, поэтому наиболее сложным стало вывести систему уравнений движения маятников. После теоретической части работы и первых прогонов на компьютере стало ясно, что необходима доработка. В дальнейшем продукт прошел множество тестирований: пересмотр формул, испытания в предельных ситуациях, проверка на сохранение энергии и, даже, на вшивость. Все тесты дали вроде бы положительные результаты. Это программа использует две полярные системы координат: статическую и динамическую. В ней также присутствует графика: она рисует маятники, которые, сцепленно вращаясь, создают иногда просто фантастические узоры. Также она отображает стержни, на которых висят грузики и неподвижный центр. Еще в ней есть функция масштабирования, которая позволит Вам посмотреть на систему издалека или вблизи. Эта программа писалась до последнего момента, а также в последний момент и после него, поэтому мы не успели провести опыты, что ставит ее (программы) правильность под вопрос.