 | ||
 | ||
 | ||
 | ||
Переславль-Залесский, 2006 год.

Изучение нематематики началось с того, что мы превращали муху в слона, выстраивали цепочку миг - час - год - век - эра, "выпекали" из теста булку, делали из луны поэта. Разгадывали шароиды, например, "Юбилей числа π или огнестрельное оружие" (пистолет), пытались придумать палиндромы (это фразы, которые читаются слева направо и справа налево одинаково), но так и не придумали.
Еще мы занимались расшифровкой текста, отсюда возникли такие знаменитые фразы как "ПФУХФУФЧХЕФ" (то есть отсутствует) и "ЖПТНЩ" (то есть формы). А Марина Петухова придумала свой шифр и закодировала текст о школе, но, к сожалению, руководитель нашего проекта А.С. Воронцов (не без помощи таблеток глюкозы!) быстренько его разгадал.
Также мы занимались тем, что заканчивали фразы известных философов, а именно: Кант: "Человек - это животное, которое умеет... смеяться", Спиноза: "Свобода есть осознанная... необходимость", Шамфор: "Всякая идея, нравящаяся большинству, является... глупостью".
Затем зашел спор о том, какая часть речи является наиболее содержательной. Мнения нашего коллектива разошлись: одни утверждали, что это имя существительное, другие, что глагол, а третьи, что имя прилагательное. А.С. Воронцов предложил проверить это следующим способом: каждому участнику проекта надо было написать, как он провел предыдущий день, используя только ту часть речи, которую считает наиболее информативной, то есть либо существительные, либо прилагательные, либо глаголы. Затем были зачитаны все эти тексты, и наш коллектив пришел к мнению, что можно обойтись без имен прилагательных, хотя без них любой текст скучный и некрасивый; без имен существительных текст возможен, но непонятен, а самым важным является глагол - он несет основную смысловую нагрузку.
Далее началось самое интересное: мы стали разбирать олимпиадные задачи по лингвистике. Для разминки предложения на испанском. Надо было понять, в каких случаях ставится es, а в каких está. Была проведена аналогия с английским языком. Это помогло, и мы выяснили, что es и está - это глаголы-связки, и es ставится, когда процесс происходит постоянно, а está, когда процесс непостоянный.
В следующей задаче мы работали с языком эсперанто (В переводе на русский - "надеющийся". Язык международного общения, разработанный в 1887 году. Для некоторых людей он является родным). Мы проанализировали слова с переводом и поняли принцип их образования. По окончанию слова, как и в русском языке, можно определить, какая это часть речи: если окончание -o - это существительное, -a - прилагательное, -ta - причастие, а окончания глаголов -as, -is, -os показывают время глагола: настоящее, прошедшее, будущее соответственно. Суффиксы придают словам особый смысл. Например, -ar- - совокупность однородных предметов, понятий: vorto - слово, vortaro - словарь; homo - человек, homaro - человечество. Также в эсперанто есть приставки. Приставка mal- полностью переворачивает смысл корня: ğojo - радость, malğojo - горе.
Следующей ступенью в изучении "нематематики" была "Первая международная олимпиада по теоретической, математической и прикладной лингвистике" (Индивидуальное соревнование" за 2003 год). В первой задаче мы столкнулись с "трансцендентальной алгеброй" (разработана в 1916 году российским ученым Яковом Линцбахом). Она, по мнению разработчика, должна была быть понятна всем людям, независимо от их родного языка.
Были даны фразы, записанные на языке Линцбаха, и их переводы на русский
язык. Фразы представляли собой набор значков. Для того чтобы понять, как
устроен язык, надо внимательно посмотреть на приведенные фразы и найти в них
сходства и отличия, из чего можно вывести закономерности - они и будут
являться грамматическими правилами данного языка.

В начале предложения ставится подлежащее. Далее идет сказуемое, которое обозначается степенью подлежащего. Знак равенства указывает на то, что у процесса есть конечный результат. После него идут второстепенные члены предложения.
Из предложения 3 видно, что конвертик - это письмо. Из 6-го и 2-го предложений видно, что молоток - это работа и производные этого слова. Посмотрев на предложение 5, мы решили, что корень обозначает слово "быть", +/-t означает время совершения действия: будущее или настоящее. Как видно из предложения 2, множественное число обозначается с помощью латинской буквы "n". Число внизу означает лицо. А то, что I - значок человека, мы догадались не сразу.
В следующей задаче было дано 5 арифметических равенств на египетском
диалекте арабского языка. Все слагаемые и все суммы, кроме последней, -
дроби, в которых ни числители, ни знаменатели не превосходят десяти, нет
также знаменателей, равных единице:

Задание: записать данные равенства цифрами.
Из равенства (5) видно, что sub۶en + xumsen это 2/7+2/5 (или в обратном порядке), отсюда следует, что окончание -en соответствует 2-ум в числителе дроби. Далее внимательно посмотрев на (1): tumn + tumnen, предположим, что отсутствие окончания соответствует единице в числителе. Мы пошли по ложному следу, одновременно пытаясь найти однокоренные слова и подобрать дроби. Попытка не увенчалась успехом, да и на подбор ушла куча времени. К счастью, А.С. Воронцов дал подсказку, что гласные в дробях арабского языка применяются для благозвучия, поэтому следует внимательнее отнестись к сочетаниям согласных букв. Мы предположили, что в дробях, состоящих из двух слов, сначала идет числитель, а потом знаменатель. Из (1) следует, что сочетание t-l-n означает 3. Из (3) получили 3(s-d-s) = 2(t-s-۶) => t-s-۶ кратно трем. Сочетания t-s-۶ и s-d-s означают 9 и 6 или 6 и 4, а t-m-n - это восемь. sub۶en + xumsen это 2/7+2/5 соответственно. Обратим внимание на равенство (2): если предположить, что s-d-s равно 4, то получим 7/3 + 1/4 = 31/12, этот вариант не подходит, так как числитель суммы превосходит 10 => s-d-s=6, а 7/3 + 1/6 = 15/6 = 5/2 = 10/4 из чего ۶-s-r равно 10, а r-b-۶ равно 4.
При разгадывании третьей задачи можно было почувствовать себя басками. Дано несколько словосочетаний на баскском языке и столько же на русском. Следовало их сравнить и найти сходства. Мы увидели, что в трех словосочетаниях на баскском и русском есть одинаковые слова, и решили сопоставить эти предложения. Появилась логическая цепочка. Дальше задача легко решалась методом рассуждений и исключений. Из этой задачи мы выяснили, что, например, larunbata по-баскски суббота, а abenduaren - декабрь.
Задача №4 оказалась не самой трудной, хотя по баллам она была второй по сложности. Были даны предложения на адыгейском языке, записанные в упрощенной латинской транскрипции. Они состояли всего из трех слов, хотя в русском переводе было от трех до пяти слов. Оказалось, что предлоги и местоимения входят в другие слова, т.е. для каждого предлога существует свое меняющееся окончание слова. Вначале были обнаружены одинаковые окончания у глаголов в вопросительных предложениях. Потом - одинаковые части слов в других предложениях. Таким образом, мы установили общий порядок слов.
В пятой задаче нас не стали мучить, и мы занялись расстановкой приставок в глаголах. Приведенная ниже таблица содержит французские глаголы с приставками и соответствующие им бесприставочные глаголы, а также русские переводы тех и других. Заштрихованные ячейки таблицы означают, что данный глагол с приставкой не имеет соответствующего бесприставочного. В некоторых глаголах приставки пропущены.
Задание: пользуясь информацией из таблицы, заполните пропуски.
| réagir | реагировать | ||
| __assortir | подбирать заново | assortir | подбирать |
| recommencer | возобновлять | commencer | начинать |
| recomposer | снова складывать | composer | складывать |
| réconcilier | мирить | concilier | мирить |
| réconforter | поддерживать | conforter | поддерживать |
| recréer | воссоздавать | créer | создавать |
| récréer | веселить | ||
| __curer | чистить | curer | чистить |
| redire | повторять | dire | говорить |
| réduire | сокращать | ||
| rééditer | переиздавать | éditer | издавать |
| refaire | делать заново | faire | делать |
| __former | реформировать | ||
| __former | образовывать заново | former | образовывать |
| __futer | опровергать | ||
| réincarner | вновь воплощать | incarner | воплощать |
| rejouer | возобновлять игру | jouer | играть |
| __lancer | снова бросать | lancer | бросать |
| __munérer | вознаграждать | ||
| rénover | обновлять | ||
| réopérer | повторно оперировать | opérer | оперировать |
| repartir | снова уезжать | partir | уезжать |
| __partir | распределять | ||
| répéter | повторять | ||
| résonner | звучать | sonner | звучать |
| révéler | раскрывать |
Выбор небольшой: re или ré. Если внимательно посмотреть на глаголы, не имеющие бесприставочной формы, можно заметить, что они имеют одинаковые приставки ré => в подобных словах с пропусками логично поставить ее же. Внимательно посмотрим на следующие слова: recommencen (возобновлять), recomposer (снова складывать), recreér (воссоздавать), redire (повторять), refaire (делать заново), rejouer (возобновлять игру) и repartir (снова уезжать), можно заметить, что значением каждого из этих глаголов является возобновление или повторение действия. Отсюда можно сформулировать правило: если надо что-то переделать или сделать ещё раз, то перед глаголом ставится re. Опираясь на него, пишем reformer (образовывать заново), relancer (снова бросать), reassortir (подбирать заново), но, внимательно посмотрев на таблицу, замечаем, что некоторые глаголы не соответствуют этому правилу: rééditer (переиздавать), réincarner (вновь воплощать), réopérer (повторно оперировать). Корень у этих слов начинается с гласной буквы, значит в слове réassortir (подбирать заново) пишем ré с аксаном. Осталось слово récurer (чистить). Оно не попадает под наше сформулированное правило => пишем ré с аксаном. Все, таблица заполнена.
Сочинение на тему "Как я провёл лето" писали
Петухова Марина и Квон Дина.
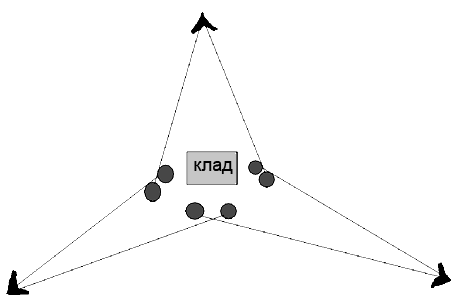
Нашему проекту "НеМатематика" по ходу учебы предагали решать всякие интересные задачки. Одной из запоминающихся задач - это "Задача про клад".
Её условие: у нас есть клад (ценная для вас вещь) и охраники, которые смотрят только в одну сторону. Поставте охраников так, чтобы вор не проник к кладу и не мог ударить охраников со спины.
Вопрос: Какое минимальное число охраников потребуеться?
Ответ: Всего 6 охраников.
Васяева Александра.
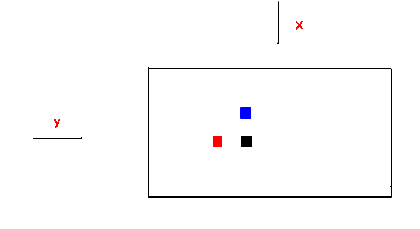
Задача про кубики заключается в том, что за столом сидят двое людей, на столе стоят кубики. Каждый видит определённую комбинацию кубов.
Условия, расположить минимальное количество кубиков так, чтобы люди не догадались, как они расположены. Как это сделать?
Если кубики расставлены так, как показано на рисунке, то ни кто не догадается о положении черного куба. Так, как красный куб загораживает обзор человеку у. Человек х не видит черный куб из-за того, что синий куб загородил его.
Таким образом, решается эта задача.
С меньшем количеством кубов задача не решается так, как два куба видны хотя бы одному человеку.
Сергей Пальков.