 | ||
 | ||
 | ||
 | ||

Авторы проекта: Влад Волокитин, Сергей Нодельман
Научный руководитель: Петр Ширков
Со-Руководители: Кирилл Лапшин, Олег Доля
В курсе физике существует несколько переходов, малопонятных для
школьников. Например, как изменение микропараметров частиц влияет на
изменение макропараметров вещества. Основные задачи проекта:
- помочь школьникам совершить этот переход, понять то, что они не поняли в школе
- вызвать у них интерес к физике (а точнее, к термодинамике)
А как это можно сделать? Нужно написать программу, моделируюшую данную
ситуацию!
В этом году участникам проекта было предложено создать математическую модель идеального газа. Мы остановились на модели идеального газа, как наиболее простой для понимания и легкой для реализации. В наш проект пришли два парня : Павел Игнатьев (Пущино) и Алексей Кузнецов (Москва). В ходе занятий были прочитаны лекции и проведены семинары по математике, термодинамике и програмированию на Турбо-Паскале.
В проекте царил дух соревнования: перед ребятами были поставлены одинаковые задачи, а машинное время (которого всегда не хватает) делилось поровну. Таким образом, каждый стремился узнать больше и сделать свою программу лучше. В итоге выиграли все : ребята многому научились, с удовольствием ходили на занятия (и собираются прийти в МКШ 6), да и основные задачи проекта были выполнены.
03.08.93. Пущино.
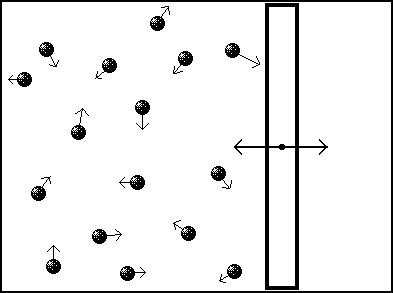
Демон Максвелла - важный элемент мысленного эксперемента крупного английского физика Максвелла. Предназначался для нападения на
второй принцип термодинамики. В мысленном эксперименте Максвелла
Демон располагается рядом с отверстием в переборке, разделяющей
сосуд, наполненный движущимися молекулами. Работа Демона состоит в
том, чтобы выпускать из одной половины сосуда в другую быстрые молекулы и закрывать отверстие перед носом медленных.Идеальный демон
способен таким образом без затраты труда создать очень высокую
температуру в одной половине сосуда и очень низкую - в другой,
осуществляя вечный двигатель второго рода.
(Аркадий и Борис Стругацкие. "Понедельник начинается в субботу")
Предметная часть проекта - термодинамика и строение вещества
- является составной частью школьного курса физики, который имеет
дело с изучением особенностей коллективного поведения огромного
числа микрочастиц и способов его описания при помощи таких макроскопических характеристик как температура, давление, энтропия. Рассмотрение такой системы с позиции Ньютоновской механики
невозможно. Однако именно механика Ньютона соответствует интуитивным представлением человека о движении. Более того, в существующих
школьных курсах физики, механический способ описания мира предшествует разделу термодинамики и к его изучению ребята приступают с
уже навязанным им "механистическим" мышлением. Именно поэтому переход к принципам статистики вызывает у школьников значительные
затруднения.
Этот проект был придуман для того, чтобы помочь школьникам интуитивно почувствовать статистическую физику. Его основная цель - ознакомить учащихся с "немеханическими" способами описания мира на возможно более ранней стадии (одновременно с изучением кинематики и механики, т.е. на уровне 7-8 класса).
Перед ребятами можно поставить задачу по созданию демонстрационных программ и программ для компьютерного эксперимента ("драйверов") с идеальным и неидеальным газом, который может подвергаться различным внешним воздействиям. Каждый драйвер должен преобразовывать движение большого числа микрочастиц в макро-свойства: давление, температуру и пр., воспроизводя все это на мониторе.
Для решения подобного рода задач учащиеся должны овладеть методологией компьютерного моделирования, или вычислительного эксперимента, который включает в себя три этапа:
- построение физической модели (выбор физических законов и
допущений, в рамках которых будет решаться поставленная
задача);
- построение математической модели (описание выбранной физической модели языком математики);
- реализация математической модели на компьютере, отладка
программы и проведение компьютерного эксперимента, по результатом которого
уточняется исходная физическая постановка.
Для выполнения этой программы Вам необходимо иметь любой учебный компьютер. Вполне достаточно, чтобы он умел считать и строить изображения (точки, отрезки), и совсем не важно какая среда программирования при этом будет использоваться: Бэйсик или Турбо-Паскаль...

Демон - маленький разумный человечек, придуманный
физиками для мысленных экспериментов над частицами, составляющими вещество.
Наша задача - смоделировать поведение вещества (газа) при различных внешних условиях и посмотреть, как, не измеряя
скорость каждой частицы, можно предсказать поведение системы в
целом. Рассчитать движение каждой молекулы даже для одного кубического
дециметра воздуха (содержащего 1023 молекул) не в состоянии самый мощный
современный компьютер. Лишь коллективное поведение частиц дает нам такие
параметры, как давление, температура, энтропия и т.д. Каждый уважающий себя физик для проверки
своих теорий ставит эксперимент. Провести реальный эксперимент
мы не в состоянии, поэтому попытаемся смоделировать поведение
газа на компьютере (поставить компьютерный эксперимент), ограничившись
небольшим числом молекул N (в пределах от 10 до 200 в
зависимости от быстродействия машины).
Цель занятия - ознакомить учащихся с отличительными особенности строения твердых тел, жидкостей и газов.
Темы для обсуждения:
1. Твердые тела, жидкости и газы.
2. Основные макро- и микро- характеристики газовых сред,
связь между ними и их характерные числовые значения: плотность,
температура, давление, размеры частиц, их средняя скорость и длина
свободного пробега, частота столкновений;
3. Простейшие газовые модели (модель идеального газа, Броуновский газ и др.) и способы их описания.
Цель занятия - проектирование и компьютерная реализация простейшего драйвера: газ в цилиндре с подвижным поршнем.
Темы для обсуждения:
1. Выбор стартовой модели газа, включая количество частиц в
рассматриваемой области: оно зависит от быстродействия компьютера.
На первом этапе мы рекомендуем ограничится плоской моделью
идеального газа, состоящего из частиц-"точек" одинаковой массы.
2. Характер движения частиц в цилиндре и способы его описания (кинематические!).
Необходимо обратить особое внимание на дискретный характер рассматриваемой математической модели: время разбивается на набор последовательных промежутков равной длины dt, для которых и записываются кинематические соотношения.
Детально разберите отражение частиц от стенок цилиндра: как меняются координаты и составляющие скорости? Для отладки программы предложите учащимся "запустить" в цилиндр только одну частицу.
Предложите учащимся самостоятельно придумать способ управления движением поршня - это необходимо для изменения объема цилиндра.
Попросите школьников оценить параметры компьютера (объем памяти и быстродействие), которые он должен иметь для моделирования поведения полного (истинного) числа частиц в 1-м кубическом дециметре воздуха при нормальных условиях в рамках выбранной ими модели.
Из курса кинематики известно, что зная скорость и координаты частицы в какой-либо
момент времени, можно определить ее положение в следующий момент. Так как
действие будет происходить в плоскости экрана, то для каждой из N частиц (их
мы будем изображать точками) необходимо знать ее координаты x, y и вектор
скорости Vx, Vy. Для простоты примем, что
все частицы имеют одинаковую массу m. Поместим их сначала в цилиндр с
неподвижными стенками, которые можно изображать отрезками прямых. Что
происходит с частицами в цилиндре? Они движутся, сталкиваясь со стенками и
между собой.
Предположим, что в момент времени t1 положение всех частиц нам
известно. Рассмотрим момент времени t2=t1+dt. Если частица ни с
чем не столкнулась, ее новые координаты будут такие:
x2 = x1+Vx·dt,
y2 = y1+Vy·dt.
В наипростейшем варианте идеального газа можно пренебречь столкновениями
между молекулами, а столкновения со стенками считать упругими. Например, в
результате столкновения с поршнем по закону зеркального отражения имеем:
Vx2 = -Vx1,
Vy2 = Vy1.
А как изменяются координаты частиц?
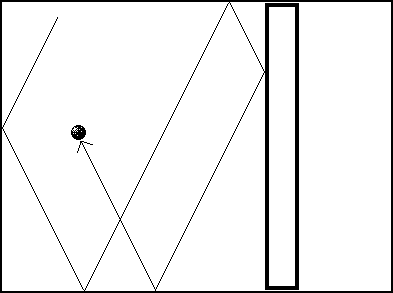
Чтобы отладить алгоритм движения, можно сначала запустить в цилиндр одну молекулу и понаблюдать за ее движением. Изображая новое положение частицы не забудьте "стереть" ее старое! От стенки до стенки она должна двигаться по прямой, а от стенок она будет отражаться зеркально.
После того, как вы отладите движение частиц, научитесь двигать поршень - это вам необходимо для изменения объема цилиндра. Здесь возможны два варианта:
- задается закон движения поршня (например, с постоянной скоростью: конечно, она должна быть существенно меньше скорости частиц газа);
- можно управлять движением поршня с клавиатуры, перемещая его за один
такт вправо или влево (это под силу тем, кто уже набил руку в программировании).
Цель занятия - установление количественных соотношений между микро- и макро- характеристиками и "создание" измерительных приборов: термометра и манометра.
Темы для обсуждения:
1. Понятие температуры газа как меры средней кинетической
энергии частиц.
2. Понятие давления газа как меры изменения импульса (количества движения) частиц при их столкновении со стенками цилиндра
(поршнем) или как меры их воздействия на воображаемую поверхность
единичной площади. При вычислении давления на поршень можно пренебречь
скоростью его движения (почему?), т.е. считать его неподвижной стенкой.
При обсуждении этого пункта обратите особое внимание на выбор
длительности времени, в течении которого подсчитывается число ударов частиц о
поршень. Как будет зависеть качество измерение давления (погрешность Вашего
манометра) от этой величины?
3. Выбор физических единиц (размерностей) измеряемых величин: массы,
времени, площади, длины. Покажите учащимся преимущества "безразмерной"
системы единиц (именно такие системы и используются, например, в
атомной физике) - m(масса частиц)=1, dt=1,
S(площадь поршня)=1,
l(длина свободного пробега)=1.
Какие размерности при этом получатся у остальных характеристик?
Давление получить несколько сложнее. Чем оно обусловлено?
Газ давит на стенки сосуда за счет того, что с ними часто и быстро сталкиваются молекулы.
Каждая частица при этом передает стенке некоторый импульс или количество движения
Dp = m·DVx
Для случая абсолютно упругого удара с боковой стенкой
DVx = 2Vx, т.е.
Dp = 2m·Vx ( но лучше пользоваться формулой (2), поскольку
в дальнейшем нам могут понадобиться не только упругие удары).
Теперь включим секундомер на время t и измерим, на сколько увеличился импульс p за счет всех ударов, произошедших за это время. Т.к. изменение импульса за единицу времени есть сила, то среднюю силу, действовавшую на поршень все это время, можно записать как F=p/t, тогда полное давление на поршень есть P=F/S=p/(S·t), где S - площадь поршня. Время t нужно выбирать аккуратно. Чем оно больше, тем точнее результат, но тем дольше считается давление P. Малость временного промежутка может привести к сильным скачкам давления даже при неизменных внешних условиях. Одна из возникающих задач - определить, почему это происходит и как выбрать t или какую-то иную временную характеристику.
Выбор физических единиц. Можно измерять массу в граммах, скорость - в метрах в секундах, а температуру - в градусах, но это приведет в конечном итоге к дополнительным ненужным коэффициентам в формулах, да и диапазоны изменения всех значений будут уж слишком непривычными (нужно вспомнить, что газ у нас достаточно "разрежен" - всего 100 молекул на весь экран). Гораздо легче положить m=1, t=1, S=1, l=1 (сами выберите единичную длину, соответствующую необходимому числу точек на экране). Отсюда автоматически получится размерность скорости и других величин. Надо сказать, что так обычно поступают и в атомной физике - там характерные значения базисных величин (масса и заряд электрона,скорость света) полагаются равными единице, поэтому все производные от них безразмерны - очень удобно!
Цель занятия - ознакомление учащихся с изотермическим процессом и моделирование этого процесса.
Темы для обсуждения:
1. Построение модели изотермического процесса. Это достаточно
просто, поскольку отсутствует передача энергии между частицами газа и стенками.
2. Компьютерный эксперимент. Построение изотермы и обсуждение
полученных результатов.
3. Построение уравнения, описывающего изотермический процесс.
Обсуждение графика P(V) (изотермы). Особо следует рассмотреть такой вопрос:
почему экспериментальные точки не попадают на теоретическую кривую? Какое
количество частиц оптимально, т.е. и эксперимент идет достаточно быстро, и
график получается достаточно точным? Что значит ДОСТАТОЧНО?
Мы сделали экспериментальную установку и сконструировали
измерительные приборы: термометр и манометр. Теперь, двигая поршень мы можем
изменять объем камеры и измерять величину давления в зависимости от объема.
Проведя достаточное количество замеров, построим соответствующий график (для
его изображения на экране выделим какую-либо область). В одном из разделов
физики - термодинамике исследуются подобные процессы и вводится уравнение,
описывающее состояние идеального газа: уравнение Менделеева-Клайперона. В
нашей "безразмерной" системе физических величин оно запишется в виде
(3)
P·V=N·T

Сопоставим эту зависимость с графиком, полученным в нашем эксперименте: как лягут наши "измеренные" точки относительно теоретической кривой (3)? (Кстати, что это за кривая?). Что изменится при другом выборе промежутка времени измерения давления? Как это объяснить? Как изменится картинка при изменении числа частиц в цилиндре? Тот, кому понравится отвечать на эти и другие подобные вопросы, а также ставить их себе самому, по праву может считать себя неплохим физиком-экспериментатором.
Попробуйте теперь "включить" столкновения частиц между собой. По какому
закону Вы будете их сталкивать? В любом случае, уравнение идеального газа,
которое изучается в школе, уже не будет верно описывать такую модель газа. Ваш
эксперимент будет точнее. Попробуйте объяснить положение экспериментальных точек
на изотерме (так называется график P(V) при постоянной температуре).
При изучении изохорического процесса, которое проводится по схеме занятия #4, следует подробно остановиться на рассмотрении модели обмена энергией (температурой) между частицей и стенкой. В простейшем случае можно воспользоваться законом теплопередачи Фурье.
Те, кто справится с этим заданием, могут переходить к моделированию изобарического процесса. При этом особое внимание придется уделить проблеме "выравнивания" давления, т.е. поддерживанию его неизменным. Можно решить ее например так: на каждом шаге считаем давление, если оно меньше Po то сдвигаем поршень влево (уменьшаем объем), если же давление больше Po то сдвигаем поршень вправо (увеличиваем объем).
Чем выше температура газа, тем выше скорости его молекул и наоборот. Но за счет чего же они могут изменять свою энергию? Конечно, за счет соударений со стенками, хотя есть и другие причины. До сих пор мы рассматривали упругие столкновения, которые не меняют энергию (то есть температуру) молекул. Значит, газ не может нагреться или охладиться. Пусть теперь стенка имеет температуру Tс. Тогда, если температура молекулы до соударения T1 < Tc, то молекула должна "нагреться" в результате столкновения, если же T1 > Tс, то - "охладиться". Этот процесс можно описать довольно грубым, но качественно правильным соотношением: (4)
T2 = T1 + k·(Tс - T1)
где k - коэффициент теплопередачи. Вспомнив, что T = m·V2/2 = m·(Vx2+Vy2)/2, вы без труда получите необходимые формулы вычисления Vx и Vy для "обработки" столкновений. Если k=1, то молекула мгновенно (за один удар) "нагреется" до температуры стенки. Если k=0, то газ не будет "чувствовать", что температура цилиндра как-то меняется. Попробуйте изменять k и посмотрите, как быстро температура газа становится равной температуре стенки. Этот процесс называется переходом к термодинамическому равновесию.
Получив возможность нагревать и охлаждать газ, можно строить зависимости P(T) или P(V) и сравнивать их с теоретической формулой (3). Попробуйте учесть столкновение между молекулами аналогично формуле (4). Как это повлияет на скорость установления термодинамического равновесия? А, может быть, вам удастся построить лучшую, чем (4) модель передачи тепла?
Вы познакомились с основами моделирования термодинамических систем на компьютере. Возможности нашей установки далеко не исчерпаны:
1. Можно поместить в цилиндр очень тяжелую частицу (M=100·m) и разрешить остальным об нее стукаться. Пусть частица оставляет видимый след, и вы сможете понаблюдать за рисуемыми ей интересными траекториями (это то, что в физике называется Броуновским движением). Как изменится характер движения "помеченной" частицы, если она имеет ту же массу, что и остальные?
2. Можно запустить в цилиндр сразу два газа: частицы одного будут тяжелее частиц другого(изобразите их разным цветом). Как будут отличаться их скорости?
3. Можно запустить в цилиндр два газа, но так, чтобы в начале они не были перемешаны: каждому газу отвести половину цилиндра. И можно будет наблюдать процесс их перемешивания - диффузию.
4. Поместите в цилиндр взаимодействующие частицы с разной
скоростью. Постройте функцию распределения частиц по скоростям - т.е.
количество частиц, имеющих абсолютное значение скорости в интервале
Влад Волокитин, Олег Доля, Кирилл Лапшин, Сергей Нодельман, Петр Ширков
К сожалению, трагические обстоятельства, оборвав весной 1993г. жизнь Влада Волокитина, одного из авторов идеи "Демонов", не позволили молодому талантливому педагогу и ученому довести до методического завершения начатую работу. Посвящая этот материал его светлой памяти, мы предполагаем и в дальнейшем знакомить Вас другими фрагментами компьютерного практикума.