 | ||
 | ||
 | ||
 | ||
Лето 2007, Пущино.
Овчинников Михаил, Подоляко Фёдор
Изначально целью нашей работы было моделирование силовых линий точечных зарядов, распложенных заданным образом на плоскости. Силовыми линиями (линиями напряженности) называются линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности электростатического поля в этой точке.
Даная задача была решена в первый день следующим методом: мы смотрели
направление напряженности электростатического поля (далее нэсп) рядом с
зарядом, затем по направлению нэсп отодвигались на изначально заданное
Dr,
после чего вновь пересчитывали направление силовых линий и повторяли операцию
до тех пор, пока силовая линия либо не попадет в окрестность другого заряда,
либо не выйдет за границы экрана. Напряженность электростатического поля
рассчитывалась по формуле
| E = | 1
|
n S i=1 |
qi
|
·ri, |
Количество линий, которые отрисовывались от заряда, было пропорционально самому заряду. От положительных и отрицательных зарядов линии рисовались разным цветом. Так как по определению силовые линии идут от положительных зарядов к отрицательным, то отрисовка линий нэсп от отрицательных зарядов происходила в противоположную сторону от направления нэсп.
В процессе решения данной задачи были написаны 2 программы на языке Pascal (Quls и Gen): первая была, собственно, решением поставленной задачи, а вторая - позволяла создавать случайным образом на плоскости заданное количество зарядов, что позволяло упростить задачу при вводе довольно большого количества точечных зарядов.
Развитием данной задачи стало помещение на плоскость, где были расположены точечные заряды, пластины, сделанной из метала. При решении данной задачи использовались следующие свойства металла: металл является эквипотенциальной поверхностью (на поверхности металла значение потенциала одинаково), тангенциальная составляющая нэсп на поверхности металла равна 0, следовательно, линии нэсп должны быть перпендикулярны поверхности металла; также учитывался закон сохранения зарядов. Потенциал
| E = | 1
|
n S i=1 |
qi
|
Изначально планировалось решать данную задачу следующим образом: разбить поверхность металла на маленькие кусочки, посчитать в каждом из них потенциал и в зависимости от разницы потенциалов между соседними кусочками перемещать заряд. Когда же потенциал ячеек переставал отличаться друг от друга на какую-то изначально заданную величину, индуцированные на поверхности металла заряды (их координаты и значения) передавались в уже написанную программу и отрисовывались вместе с внешними зарядами. Однако результат работы данной программы, написанной на С++, не совпадал с ожидаемым - полученные картинки противоречили физическим законам. Вероятной причиной неудачи являлось то, что отрисовка проводилась исходя из направлений несп, а расчет индуцированных зарядов - в зависимости от разности потенциалов на поверхности металла.
Следующим нашим шагом была программа, также написанная на С++. Существенное отличие её от предыдущей заключалось в том, что расчет индуцированных зарядов проводился следующим образом: между ячейками, в которых индуцировался заряд, рассчитывалась нэсп, в зависимости от её направления и величины заряд перемещался из одной ячейки в другую, то есть с физической точки зрения при помещении металла в эсп, на его поверхности возникал ток. При расчете нэсп между ячейками учитывались 2 соседние ячейки и внешние заряды. После изначально заданного количества операций, отвечающих за перераспределение зарядов, полученные индуцированные заряды отрисовывались вместе с внешними по приведенному выше алгоритму.
Результаты, полученные данной программой, совпадали с ожидаемыми и отвечали физическим законам. Написанная программа (Electrostatic) позволяла рисовать силовые линии нэсп для точечных зарядов, для точечных зарядов с расположенной между ними пластинкой металла, при этом силовые линии могли рисоваться как от внешних зарядов и индуцированных, так и только от внешних. Рисование проводилось в файл формата wmf.
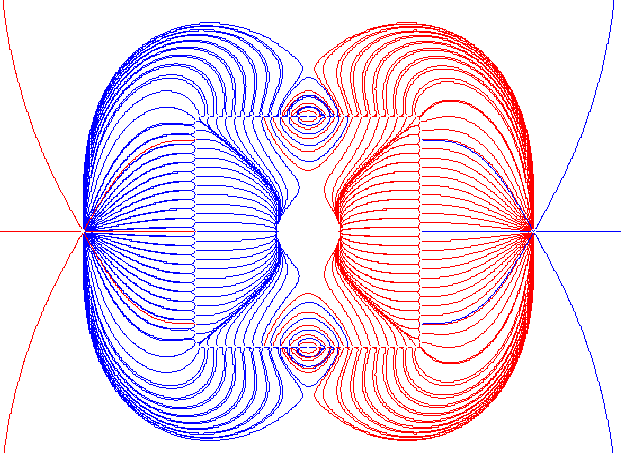
(И хоть бы кто мне сказал спасибо за использование моей либы для экспорта WMF. А, ну и пофиг — ИСН)
Накипов Руслан
Акопян Артур
Бородин Марк
Ашин Данила
За первую рабочую неделю мы смоделировали полет камня, брошенного под углом к горизонту, в программе PASCAL. По ходу выполнения этой задачи мы сделали несколько пробных программ, например программу по вычислению факториала числа или по определению типа треугольника и возможности его построения. Эти промежуточные программы были сделаны с целью изучить основы работы в Pascal'е.
Рассмотрим подробнее задание с камнем:
Мы задали начальные координаты x0, y0 и начальную скорость по оси X - Vx0 и по оси Y - Vy0.
Разобьем время на маленькие отрезки продолжительности Dt. Пусть t1 является началом шага по времени, а t2 - концом (Dt = t2 - t1).
Сначала выясним, чему равны координаты по формулам:
x(t2) = x(t1) + Vx(t1)Dt;
y(t2) = y(t1) + Vy(t1)Dt.
Теперь найдем скорость:
Vy(t2) = Vy(t1) - gDt;
Vx(t2) = Vx(t1).
Из школьного курса мы знаем, что у этой задачи есть точное решение:
x(t) = x0 + Vx0t;
y(t) = y0 + Vy0t - 1/2·gt2;
Vx(t) = Vx0;
Vy(t) = Vy0 - gt.
Учитывая условия задачи, мы также можем вычислить общее время полёта, максимальную дальность и высоту полёта. Для случая старта с земли будут верны эти формулы:
T = 2Vy0/g;
xmax = 2Vx0Vy0/g;
ymax = Vy02/2g.
Итог: мы аналитически решили задачу с камнем, брошенным под углом к горизонту, а также смоделировали его полет с помощью численного моделирования. Решение, полученное численным методом, совпадает с аналитическим решением при Dt стремящимся к 0.
07.07.
Акопян Артур
Накипов Руслан
Дергунов Сергей
Хромов Алексей
Второй задачей нашего проекта было смоделировать движение 3 трех небесных тел: Солнца, Земли и Луны. Мы ввели прямоугольную систему координат и поместили Солнце в середину экрана. Затем мы ввели массы Солнца (2·1030 кг) и Земли (6·1024 кг), скорость вращения Земли вокруг Солнца (2.97·104 м/с), и расстояние между ними (1.496·1011 м).
Поделили время на отрезки величиной Dt
t = t + Dt
На каждом отрезке мы вычисляем ускорение Земли по формулам:
axз = g·mс·(xс - xз)/r3 - по оси X;
ayз = g·mс·(yс - yз)/r3 - по оси Y.
А также скорость Земли по формулам:
Vxз = Vxз + axз·Dt - по оси X;
Vyз = Vyз + ayз·Dt - по оси Y.
И координаты Земли по осям по формулам:
xз = xз + Vxз·Dt - по оси X;
yз = yз + Vyз·Dt - по оси Y.
После мы вычислили ускорение Солнца по формулам, аналогичным Земле.
Позже мы добавили Луну. Моделировали ее движение по тем же формулам что и остальных тел.
Так как расстояние от Луны до Земли гораздо меньше расстояния от Земли до Солнца, координаты Земля и Луна на экране просто совпадают. Поэтому нам пришлось изменить экранные координаты Луны, увеличив расстояние от Земли до Луны на экране в l раз:
xл = xз + l·(xл - xз);
yл = yз + l·(yл - yз).
Вывод: построенная модель солнечной системы на наш взгляд правдоподобно описывает движение Земли, Солнца.