 | ||
 | ||
 | ||
 | ||

Руководители проекта: Березин Андрей Всеволодович, Петухов Матвей Андреевич.
Участники: Подоляко Федор Сергеевич (10 класс), Бурукин Максим Сергеевич (10 класс).
Особая благодарность: Воронцов Александр Сергеевич, Алексеев Вадим Юрьевич, Лысов Иван Дмитриевич, Стрекаловский Александр Олегович.
Место проведения: г. Переславль, Ярославская область.
Время проведения: июль-август 2006 года.
Проект МатФизика занимался реализацией математических моделей на
компьютере. При этом сплошное физическое тело заменялось моделью,
состоящей из массивных узлов, соединенных невесомыми жесткими стержнями.
Вычисления проводились пошагово с использованием математических методов
первого порядка (например:
x = x0 + vx·Dt).
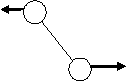
Первоначальной целью было избрано написание программы, которая моделировала бы на плоскости полет палки. Моделью палки была выбрана конструкция из двух шаров различной массы, находившихся на расстоянии L. Один шаг данной программы состоит из следующих стадий:
При таком способе моделирования выполняются законы сохранения импульса и момента импульса.
Исходники программы: palka.pas
Логическим продолжением данной программы стало моделирование полета плоского тела на плоскости. В качестве модели плоского тела была выбрана конструкция из 4х шариков, образующих квадрат. С экрана задавались следующие величины: массы шариков, длина стороны и первоначальные скорости каждого шарика по двум осям. Для реализации этой задачи необходимо было учесть не только силу упругости, но и законы сохранения импульса и момента импульса (кинетического момента) (
|
Исходники программы: kvadr.pas
Исходя из полученных результатов, мы перешли к моделированию
трехмерного тела (коробки).
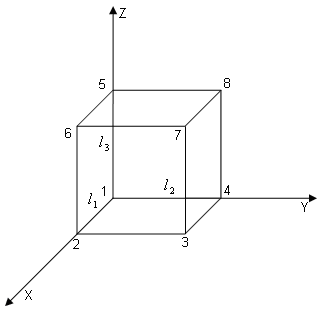
Основной алгоритм программы:
x = x0 + vx·Dt
y = y0 + vy·Dt
z = z0 + vz·Dt
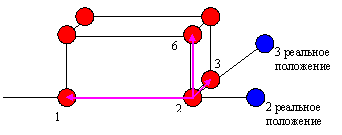
|
|
Аналогично действуем для проекций на другие оси.
| ||
| ||
|
Решаем следующее уравнение относительно омеги; получаем угловую
скорость, которой не хватает для сохранения кинетического момента.
|
Переводим угловую скорость в линейную: v = [wr]
и добавляем её к каждому шарику.
| |
| |
|
Исходники программы: box.pas
Промежуточным итогом стало моделирование вращение коробки вокруг средней оси. В отличие от вращения относительно длинной и коротких осей, это вращение является неустойчивым, т.е. ось вращение меняет свое местоположение в координатах коробки.
Затем программа была изменена таким образом, чтобы рисовать направление вектора угловой скорости и его изменение в процессе вращения коробки. Полученная траектория движения - система, состоящая из 2х эллипсоидов.
С точки зрения физики это означает, что при небольшом смещении вектора омега (угловой скорости) из устойчивого положения, ось вращения почти не изменяется.
При больших сдвигах ось вращения описывает эллипс вокруг устойчивого положения. При смещении вектора угловой скорости из неустойчивого положения, траектория её движения резко изменится.
Участники группы: Сергей Крылов(8-й класс), Сергей Дергунов(7-й класс).
Место: Переславль.
Время: 2006-08-04.
Задача 1. (полёт тела, брошенного вертикально вверх)

Первой поставленной задачей было моделирование полёта тела, брошенного вертикально вверх. Тело начинает движение из точки (у = 0) с известной скоростью (v0). Шаг по времени (dt) и ускорение свободного падения (g) являются параметрами задачи.
Уравнения движения за шаг по времени (dt) имеют вид:
v = v - g*dt;
y = y + v*dt.
Знак "-" перед (g) объясняется направлением оси (y)
вертикально вверх (рис. 1). Когда (у) равно нулю, программа
заканчивает свою работу.
Задача 2. (полёт тела, брошенного под углом к горизонту)

Второй поставленной задачей было моделирование полёта тела, брошенного под углом (a) к горизонту. Тело начинает движение из точки (x=0, у=у0) с известной скоростью (v0). Шаг по времени (dt) и ускорение свободного падения (g) являются параметрами задачи.
Уравнения движения за шаг по времени (dt) имеют вид:
vy = vy - g*dt;
y = y + vy*dt;
x = x + vx*dt;
vx = vx (Скорость по х остаётся постоянной).
Начальные скорости определяются по формулам:
vx0 = v0*cos(a);
vy0 = v0*sin(a).
Программа заканчивает свою работу, когда (у≤0) и (vy<0).
Задача 3. (одномерный пружинный маятник)
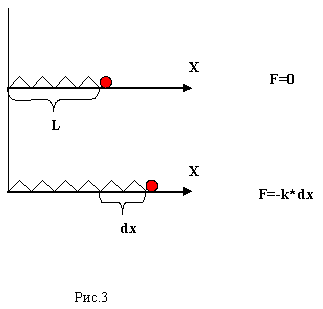
Третьей задачей было моделирование движения тела массой (m), прикреплённого к невесомой пружине. Пружина в нерастянутом состоянии имеет длину (l). В сжатом состоянии пружина действует с силой (F=k*dx) (рис.3), где (k) - коэффициент жёсткости, (dx) - деформация пружины.
Начальное положение тела характеризуется координатой (x) и начальной скоростью (v).
Уравнение для вычисления силы:
f = - k*(x - l).
Уравнение для вычисления ускорения:
a = f/m.
Уравнения движения:
v = v + a*dt;
x = x + v*dt.
Время меняется по формуле:
t = t + dt.
Программа заканчивает свою работу, когда время достигает заданной величины.
Задача 4. (двумерный пружинный маятник)
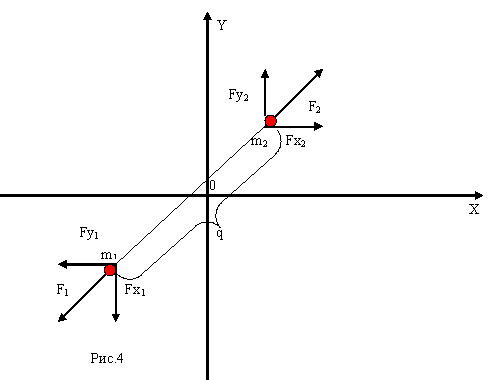
Четвёртой поставленной задачей было моделирование движения двух тел, прикреплённых к невесомой пружине. Пружина в нерастянутом состоянии имеет длину (L), в деформированном состоянии - (q). Начальными данными являются: массы тел (m1, m2), начальные скорости (v1, v2) и начальные координаты двух тел. Длина пружины (l), коэффициент жёсткости пружины (k) и шаг по времени (dt) являются параметрами задачи.
Координаты вектора, направленного из точки (x1, y1)
в точку (x2, y2):
x = x2 - x1;
y = y2 - y1.
Длина пружины в деформированном состоянии:
| q= | Ц |
x2+y2
|
Сила натяжения пружины:
F = k(q - L).
Уравнения силы для первого тела:
F1 = F/2;
Fx1 = F1*x/q;
Fy1 = F1*y/q.
Уравнения силы для второго тела:
F2 = -F/2;
Fx2 = F2*x/q;
Fy2 = F2*y/q.
Уравнения ускорения для первого тела:
ax1 = Fx1/m1;
ay1 = Fy1/m1.
Уравнения ускорения для второго тела:
ax2 = Fx2/m2;
ay2 = Fy2/m2.
Уравнения скорости первого тела:
vx1 = vx1 + ax1*dt;
vy1 = vy1 + ay1*dt.
Уравнения скорости второго тела:
vx2 = vx2 + ax2*dt;
vy2 = vy2 + ay2*dt.
Координаты первого тела:
x1 = x1 + vx1*dt;
y1 = y1 + vy1*dt.
Координаты второго тела:
x2 = x2 + vx2*dt;
y2 = y2 + vy2*dt.
Далее расположены графики зависимости длины пружины от времени, полученные в четвёртой задаче.
В первом случае шарикам придали скорости, направленные вдоль пружины (по оси X). Средняя длина пружины в этом случае равна длине пружины в недеформированном состоянии.
Во втором случае шарикам придали противонаправленные скорости, перпендикулярные пружине (по оси Y). Пружина вращается, при этом её средняя длина больше длины в недеформированном состоянии.
Это объясняется тем, что для вращения шариков нужно, чтобы на них действовала центростремительная сила. В данном случае центростремительной является сила упругости, действующая на шарики со стороны пружины. Именно поэтому вращающаяся пружина удлинена относительно движущейся прямолинейно.
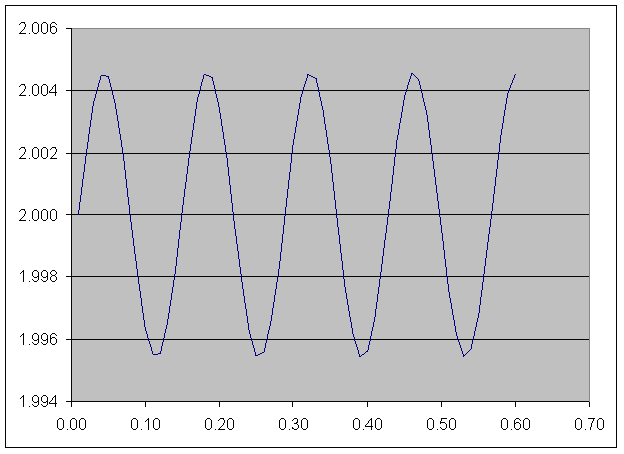
график 1
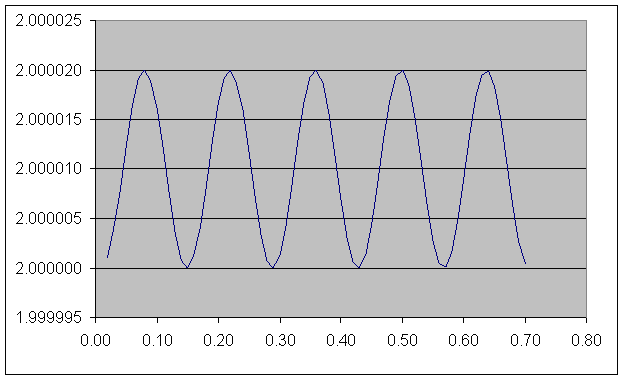
график 2