 | ||
 | ||
 | ||
 | ||
Участники:
Воронцов Илья, 9-й класс.
Пищугина Елена, 9-й класс.
Савельянов Даниил, 7-й класс.
Заболотский Андрей, 7-й класс.
Сазонов Константин, 7-й класс.
Преподаватели:
А. Березин.
И. Шитова.
Для каждого натурального числа, начиная с двойки, проводят следующие действия: выписываются по возрастанию все возможные остатки от деления на него, кроме 0, возводятся в некоторую выбранную степень и берутся по модулю этого числа. Получившиеся числа составляют один ряд треугольника остатков степеней.
Пример: построение треугольника остатков квадратов.
I этап.
2 1
3 1 2
4 1 2 3
5 1 2 3 4
6 1 2 3 4 5
...
II этап.
2 1
3 1 4
4 1 4 9
5 1 4 9 16
6 1 4 9 16 25
...
III этап.
2 1
3 1 1
4 1 0 1
5 1 4 4 1
6 1 4 3 4 1
...
То есть x(n;k)=n2k
(здесь и далее нижним индексом обозначается операция взятия по модулю), где n - это номер числа в ряду, равный исходному значению числа, x - само число, стоящее в треугольнике, а k - номер ряда (первый ряд отсутствует, т. к. единственный возможный остаток от деления на 1 - это не рассматриваемый нами 0). Эта формула годится только для треугольника остатков квадратов, для получения формулы для построения треугольников остатков других степеней надо подставить на место второй степени нужную.
Симметричность легко доказывается: пусть k - номер ряда, а m - некоторое число, не большее k-1 и не меньшее 1. Тогда
(k-m)2k=(k2-2km+m2)k= (k(k-2m)+m2)k=m2k.
В рядах, номера которых кратны 4, симметрична ещё и каждая половина ряда в отдельности:
(2k-m)24k=(4k2-4km+m2)4k= (4k(k-m)+m2)4k=m24k
(здесь доказывается симметричность левой половины ряда, но симметричность всего ряда уже доказана, и доказывать её же для правой половины нет необходимости).
Был разработан алгоритм, возможно, позволяющий генерировать очередную строку треугольника без использования стандартного способа его построения.
Возьмём число x(k;1)=1 (пусть, к примеру, k=5). Далее, вычтем из числа x(k;1) число k-2 (в нашем случае 1-(k-2)=1-(5-2)=-2). Так как число получилось отрицательное, то возьмём его по модулю k+1 (у нас получится 4) и впишем на место числа x(k;2). Вычтем теперь из результата число k-3 вместо k-2 (для случая, описанного в примере, k-3=2). Далее действуем по алгоритму: если после очередного вычитания из числа x(a;b) получаем неотрицательное число, то записываем его как x(a+1;b+1); иначе берём результат по модулю числа a+1 и в следующем вычитании уменьшаем вычитаемое (которое изначально было равно k-2) на единицу. Ясно, что тогда рано или поздно вычитаемое станет равным нулю, и последовательность зациклится (так и происходит).
Составлена (но не доказана) рекуррентная формула:
x(k;n)=(x(k-1;n-1)-(x(k-2;n-2)-x(k-1;n-1))k-2)k
До пятидесятого ряда включительно она работает, далее она ещё не проверялась. Чтобы с её помощью можно было вычислять вторые числа в каждом ряду (первые, очевидно, везде единицы), можно считать, что в начале любого ряда присутствует 0 (строго говоря, так оно и есть).
(рассматривается только треугольник остатков квадратов, но те же преобразования возможны и для треугольников других степеней).
Если провести с числами, из которых состоит треугольник, операцию возведения в квадрат и взятия по модулю (тогда, кстати, получится треугольник остатков четвёртых степеней), то одинаковые числа в разных рядах могут вести себя по-разному. Например, единица не изменится ни в каком ряду, а четвёрка останется прежней в ряду номер 6, станет двойкой в ряду номер 7 и единицей в пятом ряду. Таким образом меняется вид всей строки. А если ещё раз провести возведение в квадрат и взятие по модулю (назовём такую операцию "эволюцией"), то некоторые строчки вернутся к прежнему виду. В связи с этим интересно разделить все ряды на классы:
Несмотря на то, что это направление почти не изучено, уже известны классы рядов, переходящих в периодичные (попеременно меняют свой вид на получившийся то после первой "эволюции", то после второй, но никогда не возвращаются к исходному) и периодичные с периодом 4 (цикл состоит не из двух различных видов ряда, а из четырёх).
Кроме того, есть предположение относительно рядов с номерами, являющимися степенями двойки. Пусть номер данного ряда равен 2S, причём 2i<S≤2i+1. Тогда достаточно i "эволюций", чтобы ряд стал стабильным. При этом он приобретает вид: 1010...101, всего 2S-1 цифр (тогда можно вводить классы рядов, переходящих в стабильные со второго, третьего и т. д. раза).
Что же касается конкретных и точно потверждённых данных об этом свойстве строк треугольника, то есть следующие данные:
28.07.04, г. Переславль-Залесский.
СЛОН, проект "Геометрия".
Заболотский Андрей.
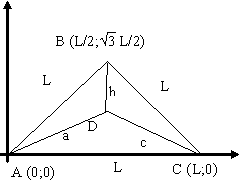
Дан равносторонний треугольник со стороной L. Есть точка, удалённая от вершин на расстояния a, b и c. A, b, c и L - натуральные числа.
Выберем систему координат, так что точка A совпадает с началом координат, а сторона AC треугольника лежит на оси OX (рис.1).
Поставим точку D(x;y). Выразим длины a, b и c и напишем систему уравнений:
|
|
|
Раскроем скобки и заменим x2+y2 на a2:
b2 = a2+L2-xL-Ц3yL
c2 = L2+a2-2xL
Выразим x и y
|
|
Подставим x и y в уравнение a2=x2+y2 и упростим выражение. Получаем выражение, симметричное относительно всех 4 переменных:
a4 + b4 + c4 + L4 = a2b2 + a2c2 + a2L2 + b2L2 + b2c2 + c2L2 (1)
Уравнение (1) абсолютно симметрично относительно всех переменных: за a, b, c или L могут быть выбраны любые расстояния.
Это уравнение имеет множество решений. Путём компьютерного перебора было получено несколько из них. Например, {3, 5, 7, 8}, {7, 8, 13, 15}.
Установлено, что:
Рассматривались только варианты, когда числа взаимно просты, так как в другом случае мы получаем другое, неизвестное решение уравнения, умноженное на НОД значений переменных.
При возведении в квадрат число возможных остатков от деления значительно уменьшается, а потому удалось проверить эти результаты, а полный перебор возможных комбинаций различных остатков подтвердил их. То, что наименьшим натуральным решением уравнения являются числа 3, 5, 7 и 8, тоже вряд ли случайное совпадение.
Пример: проверяем уравнение (1) на делимость на 2.
Существуют только два возможных остатка от деления на 2 - 0 и 1, причём при возведении числа в квадрат оно сохраняет свою чётность.
Рассмотрим вариант, при котором три числа чётные, а одно - нечётное (назовём такой вариант "0001"). В этом случае в левой части уравнения (1) присутствует одно нечётное слагаемое, т. е. эта часть уравнения нечётна, а в правой - ни одного, так как в каждом из слагаемых в качестве множителя есть квадрат чётного числа. Отбросим вариант 0001.
Рассмотрим теперь вариант 0011 (по два чётных и нечётных числа). В этом случае в левой части уравнения (1) 2 нечётных слагаемых, т. е. остаток от деления на 2 равен 0, а в правой - одно (произведение квадратов нечётных чисел). Фактически, чётное число равно нечётному, что невозможно.
Вариант 0111 реален (тогда обе части уравнения нечётны), в частности, он реализуется, когда искомая нами точка находится в вершине треугольника, т. е. когда a=0 (не обязательно a) и b=c=L=1 (или любому другому целому числу).
Вариант 0000 мы не рассматриваем (см. выше), и остаётся вариант 1111 (все 4 числа нечётные). Формально он возможен, но из этого следует, что существует вариант, при котором у всех четырёх чисел остаток от деления на 4 равен 1 или 3. Проверим, возможно ли это. В уравнении (1) каждая из переменных возводится в квадрат, при этом остаток 1 (от деления на 4) сохраняется, а остаток 3 переходит в 1. Итак, снова требуется проверить вариант 1111 - но теперь уже для деления на 4. При подстановке получаем, что в левой части уравнения 4 нечётных слагаемых (остаток 0), а в правой 6 (остаток 2). Это невозможно. Таким образом, единственный возможный вариант - 0111, то есть чётным является одно и только одно число.
Во время же компьютерного перебора в уравнение (1) подставлялись ВСЕ в принципе возможные остатки, а затем проверялось, выполняется ли равенство.
Для чисел, больших 10, ручной подсчёт невозможен, а компьютер выдаёт неудобовоспринимаемое количество вариантов, поэтому пока что больше никаких результатов получено не было.
a+b=L (2)
В этом случае для каждой тройки чисел есть два существенно различных решения: точка лежит на стороне или её продолжении (этот случай ввиду его простоты мы рассматривать не будем) и случай, когда сумма расстояний до двух вершин равна расстоянию до третьей вершины. Рассмотрим этот случай.
Упростим уравнение (1):
a4+b4+c4+L4 -2a2b2 = a2b2+a2c2+a2L2+b2c2+b2L2+c2L2 -2a2b2
(a-b)2(a+b)2+c4+L4 = -a2b2+a2c2+(a2+b2)L2+b2c2+c2L2
-2abL2+c4+L4 = -a2b2+a2c2+b2c2+c2L2
Затем выразим и подставим a из равенства (2).
Получаем уравнение b4+c4+L4+3b2L2-2c2b2-2c2L2+2bLc2-2b3L-2bL3 = 0
Замечаем, что b4+c4+L4+3b2L2-2c2b2-2c2L2+2bLc2-2b3L-2bL3 = (c2-b2-L2+bL)2
Следовательно, c2-b2-L2+bL = 0
Подставим L из равенства (2) в уравнение.
Получаем: c2 = b2+a2+ab
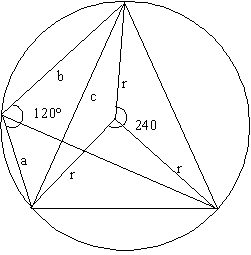
Это уравнение является полным аналогом теоремы косинусов для прилежащих сторон 'a' и 'b', противолежащей стороны 'с' и угла 120°.
Но такая точка может лежать только на описанной вокруг треугольника окружности, так как если центральный угол, как в нашем случае равен 240°, то 120° равен только внешний угол (угол лежащий на окружности) (рис.2).
Следовательно, если сумма длин расстояний от вершин до некоторой точки равна расстоянию от третьей вершины до этой точки, то эта точка лежит на описанной вокруг треугольника со стороной 'с' окружности.
Заболотский Андрей, Воронцов Илья.
29.07.04
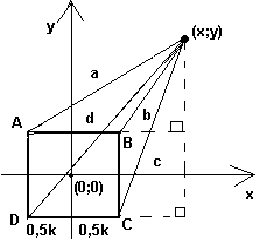
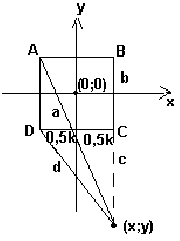
квадрат ABCD;
искомая точка с координатами (x;y);
длина стороны квадрата k;
a - расстояние от точки A до искомой точки;
b - расстояние от точки B до искомой точки;
c - расстояние от точки C до искомой точки;
d - расстояние от точки D до искомой точки;
Итог : a2-b2 = d2-c2
Итоговая система уравнений для общего случая:
a2-b2=d2-c2
a4+b4+c4+d4+3k4=(a2+c2+k2)2
На диагоналях или в углах квадрата искомой точки быть не может, т.к. диагональ квадрата равна k и любое число в сумме с иррациональным будет давать иррациональный результат.
В центре искомой точки нет, т.к. тогда a=b=c=d=(Ц2/2)k.
В центре стороны квадрата искомой точки быть не может, т.к. тогда a=d=(Ц5/2)k (число не целое).
Рассмотрим единственный частный случай, опровержение которого не найдено, но возможно, что опровержения не должно быть:
Если точка лежит на стороне квадрата или её продолжении.
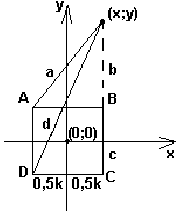
a) Случай "точка на продолжении стороны"
Вариант 1: c+k=b
b=c+k, ==> ,подставляя в уравнение для общего случая, получаем : c2+2ck+k2-a2=c2-d2
a2-d2-2ck=k2
По теореме Пифагора:
(c+k)2+k2=a2
c2+k2=d2
Получаем систему уравнений для данного вида частного случая :
2k2+2ck+c2=a2
c2+k2=d2
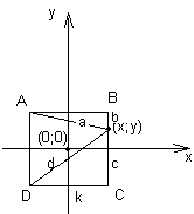
Вариант 2: b+k=c
По теореме Пифагора получаем:
(c-k)2+k2=a2
c2+k2=d2
Получаем систему уравнений для данного вида частного случая :
2k2-2ck+c2=a2
c2+k2=d2
b) Cлучай "точка лежит на самой стороне" , т.е. b+c=k
1) По условию b+c=k
По теореме Пифагора : b2+k2=a2
c2+k2=d2
2) Выразим все переменные через b и c :
k=b+c
a2=2b2+2bc+c2
d2=2c2+2bc+b2
При длине квадрата, меньшей 50, целочисленных решений найдено не было.
30.07.2004
Пищугина Елена
создать классификацию случаев, получаемых при делении треугольника на 7 частей 3-мя прямыми.
создана классификация случаев, получаемых при делении треугольника. Эта классификация учитывает различия многоугольников, получаемых в разных случаях. Далее было решено для удобства перейти к делению круга.
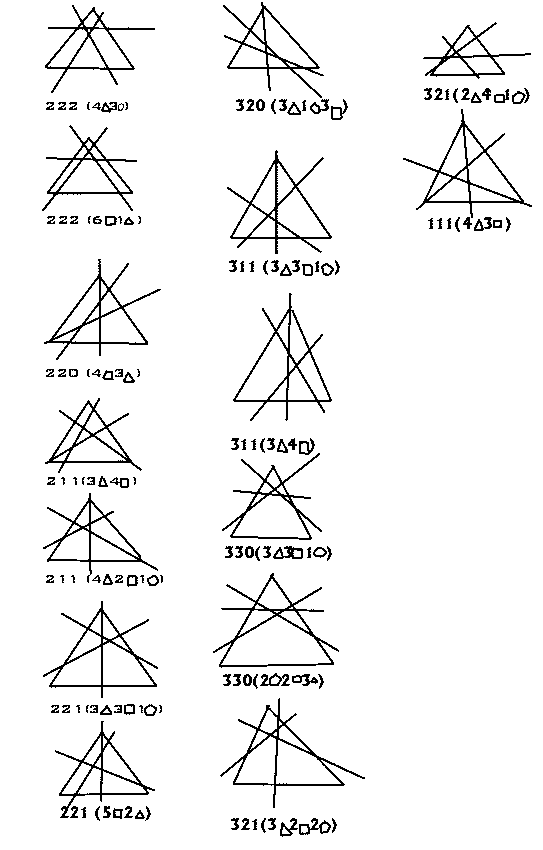
создать классификацию случаев, получаемых при делении круга на 7 частей 3-мя прямыми.
создана программа, определяющая возможное взаиморасположение максимумов и минимумов с учётом симметрии частей, основанная на выведенном участниками проекта алгоритме.
Для решения поставленной задачи мы решили составить классификацию
различных случаев количества частей, максимальных и минимальных по
площади, которые могут получиться при разрезании. Мы выяснили, что
возможны такие случаи:
1М1м
2М1м
3М1м
4М1м
5М1м
6М1м
2М2м
2М3м
2М4м
2М5м
3М3м
3М4м
Каждый случай можно реализовать множеством способов. Рисунки обозначают место расположения максимумов и минимумов. Для большинства случаев мы показали, как можно их улучшить. Для улучшения в каждом случае можно подвинуть или повернуть прямые.
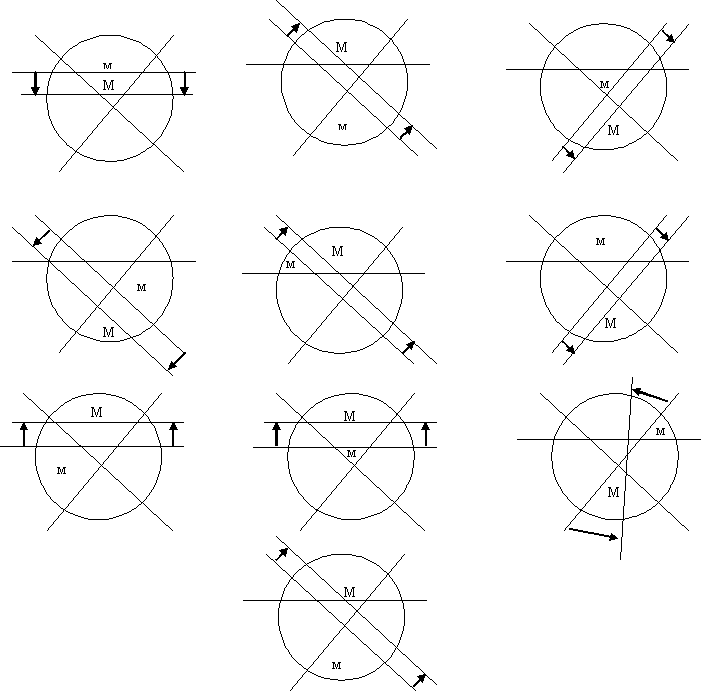
Сазонов Константин.
Участники:
Голубков Александр
Дещеревская Ольга
Петухов Матвей
Подоляко Фёдор
Поттосин Андрей
Стрекаловский Александр
Фанасков Роман
Поиск наикратчайшего пути по поверхности куба между двумя произвольно заданными точками на гранях этого куба.
Для начала мы разглядывали кубик и тыкали его булавками. Затем участники проекта рассматривали случай, при котором точки лежат на соседних гранях. Как выяснилось, в кубе не всё так просто, как кажется. Наикратчайший путь между двумя вышеупомянутыми точками может пролегать как через общее для граней, на которых лежат точки, ребро, так и через участок смежной для этих двух граней грани. Естественным образом возникает подзадача - на одной из граней дана точка, нужно найти области на другой грани, в которые выгоднее идти через общее ребро или через смежную грань. Был придуман следующий способ нахождения этих областей:
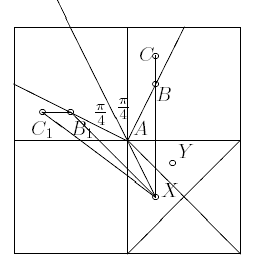
В качестве основной идеи решения было принято рассмотрение разных вариантов развёртки куба. Это позволяет рассматривать одновременно оба варианта соединения линией двух точек - через общее ребро и через смежную грань, а это, в свою очередь, ведёт к тому, что отрезок, соединяющий нужные нам точки, не разорван и его легче рассматривать.
Одна и та же грань на двух разных развёртках оказывается повёрнутой на p/2 → мы можем рассматривать одну и ту же точку на двух частях чертежа одновременно, и сравнивать разные варианты кратчайшего пути до этой точки.
Мы решили работать над задачей путём дополнительных построений - главной целью было разграничить эти области какой-то линией. Предположительно такой линией являлась совокупность точек, кратчайший путь к которым от заданной точки одинаков как через общее ребро, так и через смежную грань.
Мы провели следующие построения. Из заданной точки X через вершину A проводится луч, в точке A от него в обе стороны откладываются углы в p/4. Отрезки от точки A под p/4 к прямой XA на самом деле являются одним и тем же отрезком и их точки совпадают при повороте одной из граней на развёртке на p/2. Так как эти отрезки являются сторонами угла, биссектриссой которого является прямая XA, их точки равноудалены от X; следовательно, путь до них как через соседнее ребро, так и через смежную грань одинаков. Эти отрезки (на самом деле один отрезок, так как второй - это он самый и есть) являются границами между областями. Предположительно в одной из них выгоднее идти через общее ребро, а в другой через смежную грань.
Точки C и C1 совпадают при повороте грани на p/2,
то есть точка C1 - просто отображение точки C. Отрезок XC - это
путь через общее ребро, а отрезок XC1 - путь через смежную грань.
Но, с другой стороны, два отрезка XB1 и B1C1
в сумме дают отрезок XC, то есть сумму отрезков XB и BC, так как точка
B1 - это отображение точки B, →
Аналогично доказывается то, что в другой области, наоборот, выгоднее идти через общее ребро.
Позднее было замечено, что существует ещё одна такая граница, строящаяся аналогичным образом, из чего следует существование ещё одной области, в которой кратчайший путь лежит через смежную грань. Однако эти области ни при каком случае не пересекаются, так как даже в критическом случае они сходятся в одной точке - середине ребра.
Существует случай, когда границы нет, то есть конец отрезка, отложенного от прямой XA под p/4, попадает на сторону левого верхнего, а не правого верхнего квадрата на чертеже (то есть на грань, которой в одном из вариантов развёртки не существует). Это происходит в двух случаях. Первый обозначен на чертеже положением точки Y, то есть в четверти грани, отделённой диагоналями (верхней на чертеже). Тогда всегда выгоднее идти через общее ребро. Второй - когда точка лежит также в четверти грани, отделённой диагоналями, но в правой. Тогда нужно идти просто через другую смежную грань.
Потом мы делали вот что:
Мы решили заняться другой фигурой - тетраэдром. Все грани у него соседние, поэтому не нужно рассматривать разные случаи. Был выбран способ действий, аналогичный применённому к кубу.
Вот что получилось:
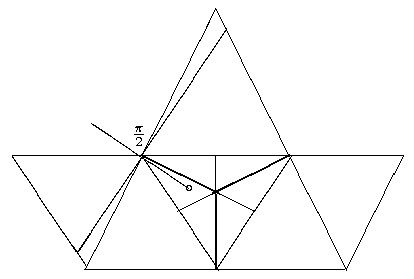
Данный чертёж - развёртка тетраэдра, в которой одна из граней повёрнута на p, в одну и в другую сторону. Все остальные построения до боли напоминают построения в кубе - из точки через вершину проводится прямая, в вершине к ней пристраиваются отрезки, правда теперь под углом p/2. На грани получается линия точек, к которым всё равно как идти - через общее ребро или через смежную грань. Аналогично задаче с кубом доказывается, что в верхней (на чертеже) области выгоднее идти через смежную грань, а в нижней - через общее ребро.
Как и в задаче про кубъ, на грани, где точка задана (на рисунке - средняя), существуют разные области. С одной стороны, можно разделить грань на две части, в которых при ситуации, когда выгоднее идти через смежную грань надо идти в различных гранях. С другой - существует область, в которой всегда выгоднее идти через ребро. Это значит, что линия, которая должна бы образовывать границу, её не образует, то есть не попадает на грань.
Таким образом, отрезок разделяющий области, в которых выгоднее идти через разные смежные зёбра, а также отрезки, отделяющие область, в которой всегда выгоднее идти через общее ребро (см. чертёж), образуют 6 областей, они соединяются по 2, и в результате получаются 3 области. На чертеже это выделено жирным. В верхней области выгоднее идти через общее ребро, а в правой и левой - через разные смежные грани, если это требуется и нельзя пройти через общее ребро.
В процессе работы проекта было создано огромное число разных интересных предметов, как то:
Также были введены новые термины, как-то:
Фёдором Подоляко были сломаны ножницы, широко использовались УПАВШИЕ со стенда таблички "Наши Достижения" и "Поздравляем".
Опытным путём было доказано то, что не бывает тетраэдров с тупыми углами, а с прямыми - они какие-то плоские.