 | ||
 | ||
 | ||
 | ||

|
|
|
Перед нашей группой была поставлена задача по созданию программы,
рисующей любой фрактал. Используя язык Pascal, мы написали ряд
алгоритмов, которые были объединены.
Итоговая программа получает на вход координаты, передаваемые
как параметры в командной строке, в которые преобразуется каждый
отрезок за один шаг. Координаты передаются в строковом виде вместе
с типом соединения. Далее они преобразовываются в массив координат.
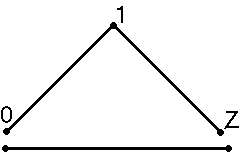
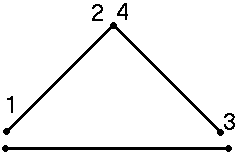
Программа имеет два типа соединения: последовательный и поточеный
(смотри рис.1 и рис.2). В первом случае в массив координат добавлялись
две точки с координатами (0,0) и (1,0), после этого все точки соединялись
последовательно. Во втором случае делалась проверка на количество точек
и нужно было добавить точки с теми же координатами, но в другом месте
массива. Отрезок отрисовывался только с нечетного номера точки и соединял
с ней следующий четный номер.
После получения этой информации программа начинала создавать точки на плоскости по заданному методу. Выполняясь до тех пор, пока между точками можно было отрисовать отрезок. Когда это было невозможно (разрешения паскаля 640*480 и начальный отрезок имеет ограниченную длину, и при этом не возможно нарисовать отрезок длиной меньше пикселя), программа начинала отрисовывать все отрезки между поставленными точками. Таким образом, можно было создать любой фрактал на плоскости, не использующий в себе комплексных чисел.
Для упрощения построения заданного фрактала мы кроме метода начальных координат начали использовать еще и интерактивный метод. После этого любой пользователь может при помощи клавиатуры изменять координаты любой точки начального отрезка относительно друг друга.
Исходники программы: univ_ver.pas
Так же были начаты эксперименты по работе с комплексными числами и написана программа, иллюстрирующая развитие множества Жюлиа при различных константах. В ней реализована возможность масштабирования и навигации по изображению. Это сделано по той причине, что при любом увеличении масштаба на "окраинах" множества существуют очень разнообразные тела, "произрастающие" из более крупных.
Исходники программы: mandel.pas
Иван Соколов, Максим Бурукин
Перед нашей подгруппой была поставлена задача реализовать частные случаи фракталов. Мы писали рекурсивные алгоритмы, которые разбивали и разветвляли отрезки по заданным правилам.
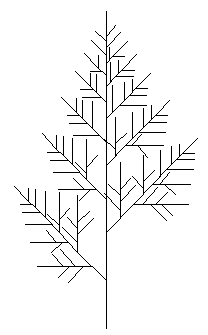
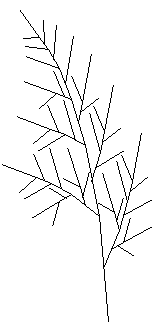
Этот алгоритм рисовал деревья. Алгоритм программы такой. Задавался начальный отрезок, он делился на несколько частей, и каждая часть рассматривалась как отдельный отрезок. Под определенным углом отходили следующие отрезки от "ствола", и т.д. В программе есть управление клавиатурой. Можно менять как масштаб всего дерева, так и различные параметры отдельных веток. Меняется угол наклона, минимальная длина веток; по нажатию пробела можно сделать цвет случайным. Тестируя нашу программу, мы узнали о нашей программе много нового: меняя различные параметры мы получали различные узоры, например, улитку, пятиугольник и т.д.

Наша самая первая программа рисовала "Кривую дракона", заменяя каждый отрезок двумя другими, достраивая его до равнобедренного прямоугольного треугольника и беря его катеты. А потом эти катеты аналогично заменялись ещё двумя и т.д. А когда отрезки достигали определённой длины, например пяти пикселей, они отрисовывались. В результате получалась "Кривая дракона". Мы заметили, что при повороте вокруг начальной точки на 90°, полученная кривая совместится с изначальной без пробелов и наложений. Поэтому мы написали программу, рисующую четыре "Кривых дракона" совмещённых таким способом, причём в ней можно было менять угол между получающимися отрезками. Для наглядности мы их сделали разного цвета.

Исходники программы: vetka.pas
Также у нас было много других частных случаев фракталов, как множество Жюлиа, салфетка Серпинского в треугольном и квадратном вариантах, остров Коха.
Оля Ким, Владимир Приказчиков
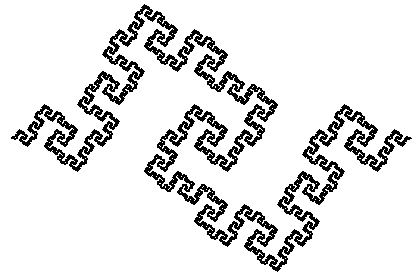













Иван Неретин