Проект 'Теория чисел'

Отчёт advanced группы (PDF):

Числа Фибоначчи - это такая последовательность чисел, в которой каждое число равно сумме двух предыдущих:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55...

Числа Лукаса - это последовательность чисел, основанная на принципе чисел Фибоначчи, только она начинается с чисел 1, 3...

День I

Искали закономерности в ряде чисел Фибоначчи.

Нашли следующие закономерности:

1) Каждое третье число - чётное.

1, 1, 2, 3, 5, 8, 13, 21, 34, 55...

2) Если порядковый номер одного числа делится на порядковый номер другого числа, то числа стоящие под ними делятся друг на друга.

F₅ = 5, F₁₀ = 55

10:5=2

55:5=11

3) При делении числа Фибоначчи с порядковым номером вдвое больше числа с порядковым номером, которое мы делим, получается ряд чисел Лукаса.

День II.

Выписывали простые числа до сотни. Написали прогу, которая могла продолжить ряд чисел Фибоначчи и прогу, которая могла продолжить ряд простых чисел.

День III

Написали прогу, которая могла показать количество и процент простых чисел в каждой сотне. Показывали это в виде графиков.

День IV

Таблица.

Число 0 1 2 3 4 5 6 7 8 9

Квадрат 0 1 4 9 6 5 6 9 4 1

n³ 0 1 8 7 4 5 6 3 2 9

n⁴ 0 1 6 1 6 5 6 1 6 1

n⁵ 0 1 2 3 4 5 6 7 8 9

Выписали последние цифры степеней. Обнаружили, что последняя цифра числа и последняя цифра 5-ой степени равны.

День V - VI

Занимались совершенными числами. Впоследствии, Олег с Севой написали программу, которая нашла 4 совершенных числа (это такие числа, которые равны сумме своих делителей, включая 1, но кроме себя.): 6, 28, 496, 8128. Разложив их на простые множетели получилось следующее: 6=2·3, 28=22·7, 496=24·31, 8128=26·127. Заметили, что числа 3, 7, 31, 127 - простые и равны степеням двойки минус 1. Дальше мы искали другие простые числа, которые могут получится если отнять от степеней двойки 1. Нашли ещё несколько таких чисел: 2¹³ - 1 = 8191, 2¹⁷ - 1 = 131071, 2¹⁹ - 1 = 524287, 2³¹ - 1 = 2147483647.

День VII-VIII

Мы сегодня находили числа Ферма. Дополнили таблицу степеней двойки.

День IX-XI

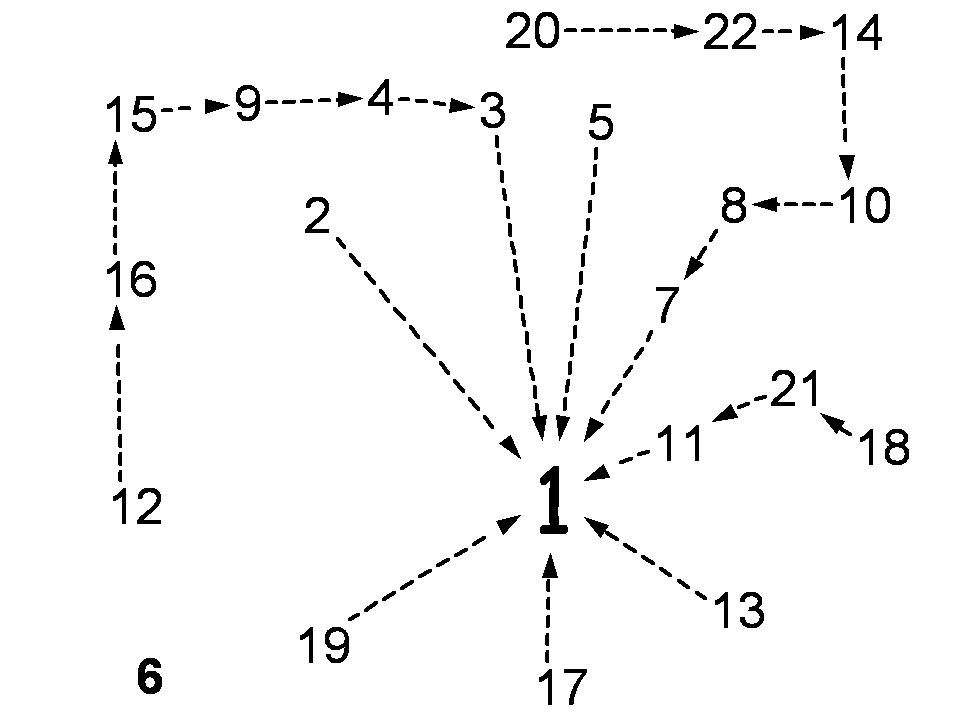
Задались вопросом, что будет если для числа посчитать сумму его младших делителей, с получившемся числом проделать тоже самое и так далее, то в большинстве случаев придём к единице. Построили "паутину" чисел (карту "московского метрополитена" 2070-х годов).

Написали прогу по вычислению периодических десятичных дробей.

Например:

1/7=0.(142857)

1/11=0.(09)

1/17=0.(0588235294117647)

Далее мы искали закономерность числа цифр в периоде. Проверили простые числа до 300 и обнаружили, что количество чисел цифр в периоде является делителем числа на 1 меньше простого, исходного числа.

Приложение 1

n	2ⁿ	2ⁿ -1	Разложение	2ⁿ+1	Разложение
1	2	1	-	3	Простое
2	4	3	Простое	5	Простое
3	8	7	Простое	9	3²
4	16	15	3·5	17	Простое
5	32	31	Простое	33	3·11
6	64	63	3²·7	65	5·13
7	128	127	Простое	129	3·43
8	256	255	3·5·17	257	Простое
9	512	511	7·73	513	3³·19
10	1024	1023	3·11·31	1025	5²·41
11	2048	2047	23·89	2049	3·683
12	4096	4095	3²·5·7·13	4097	17·241
13	8192	8191	Простое	8193	3·2731
14	16384	16383	3·43·127	16385	5·29·113
15	32768	32767	7·31·151	32769	3²·11·331
16	65536	65535	3·5·17·257	65537	Простое
17	131072	131071	Простое	131073	3·43691
18	262144	262143	3³·7·19·73	262145	5·13·37·109
19	524288	524287	Простое	524289	3·174763
20	1048576	1048575	3·5²·11·31·41	1048577	17·61681
21	2097152	2097151	53·61·647	2097153	3²·43·5419
22	4194304	4194303	3·23·89·683	4194305	5·397·2113
23	8388608	8388607	47·178481	8388609	3·2796203
24	16777216	16777215	3²·5·7·13·17·241	16777217	97·257·673
25	33554432	33554431	31·601·1801	33554433	3·11·251·4051
26	67108864	67108863	3·2731·8191	67108865	5·53·157·1613
27	134217728	134217727	7·73·262657	134217729	3⁴·19·87211
28	268435456	268435455	3·5·29·43·113·127	268435457	17·15790321
29	536870912	536870911	233·1103·2089	536870913	3·59·3033169
30	1073741824	1073741823	3²·7·11·31·151·331	1073741825	5²·13·41·61·1321
31	2147483648	2147483647	Простое	2147483649	3·715827883
32	4294967296	4294967295	3·5·17·257·65537	4294967297	641·6700417

Приложение 2

n	10ⁿ	(10ⁿ-1)/9	Разложение	10ⁿ+1	Разложение
1	10	1	-	11	Простое
2	100	11	Простое	101	Простое
3	1000	111	3·37	1001	7·11·13
4	10000	1111	11·101	10001	73·137
5	100000	11111	41·271	100001	11·9091
6	1000000	111111	3·7·11·13·37	1000001	101·9901
7	10000000	1111111	239·4649	10000001	11·909091
8	100000000	11111111	11·73·101·137	100000001	17·5882353
9	1000000000	111111111	3²·37·333667	1000000001	7·11·13·19·52579
10	10000000000	1111111111	11·41·271·9091	10000000001	101·3541·27961

• Главная	• Ворота • Миссия • О сайте
• О нас	• Преподаватели • Регламент • Традиции
• Текущее	• Лента новостей • Гостевая книга
• История	• Летопись • Проекты • Участники • Архивы • Музей
• Ссылки

Число	1	2	3	4	5	6	7	8	9
Квадрат	1	4	9	6	5	6	9	4	1
n³	1	8	7	4	5	6	3	2	9
n⁴	1	6	1	6	5	6	1	6	1
n⁵	1	2	3	4	5	6	7	8	9