| ||
 | ||
 | ||
 | ||
Итак, наша цель – моделирование падения костей домино.
В первую очередь необходимо создать модель. Наша модель – абсолютно плоские доминошки, прикрепленные одним концом гвоздиками к стенке. Поэтому отсутствует проскальзывание. Трение, турбулентность и случайные флуктуации также не учитываются.
Что можно сказать о законах, по которым падают доминошки? При падении без столкновения, очевидно, будет выполняться закон сохранения энергии. При столкновении – закон сохранения момента импульса. Также будет выполняться условие соприкосновения доминошек, так как друг сквозь друга они пройти не могут.
Обозначения:
α - угол наклона доминошки. Отмеряется от поверхности стола.
ω - угловая скорость доминошки.
ω’ – новая угловая скорость доминошки.
l – половина длины доминошки
d - расстояние между доминошками.
k- количество доминошек.
kt - количество доминошек, рассматриваемых на данный момент.
E- энергия.
J – момент инерции доминошки.
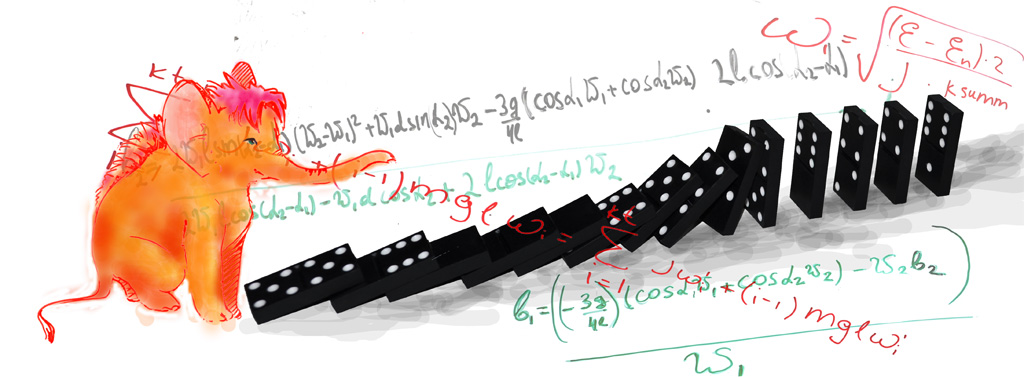
Закон сохранения энергии:
![]()
С законом сохранения моментов импульса не все так просто. По идее он должен выглядеть так:
![]()
То есть момент импульса для каждой доминошки должен считаться относительно гвоздика первой доминошки. Однако программа с такой формулой фатально не работает. Зато, если считать момент импульса для каждой доминошки относительно ее собственного гвоздика, что неправильно, все работает замечательно. Поэтому в программе закон сохранения моментов импульса выглядит так:
![]()
Условие соприкосновения двух доминошек:
Сравним результаты моделирования и экспериментальные результаты.
|
№ |
d,мм |
k |
T экс , с |
T мод , с |
Тэкс-Тмод/Тэкс |
|
1 |
10 |
82 |
1,12 |
0,8 |
28% |
|
2 |
15 |
56 |
1,2 |
0,81 |
32% |
|
3 |
20 |
51 |
1,36 |
0,937 |
30% |
|
4 |
25 |
25 |
0,88 |
0,678 |
23% |
|
5 |
30 |
53 |
2,1 |
1,5 |
28% |
Результаты моделирования, мы считаем, достаточно неплохие. Т.к. в модели не учитывалась потеря энергии в результате действия силы трения, логично, что моделируемые доминошки падают быстрее.